On this page you can find examination questions from the topic of algebra


In an arithmetic sequence, the first term is 4 and the third term is 16.
a) Find the common difference
b) Find the 8th term
c) Find the sum of the first 8 terms
Hint
a) How many differences are there between the first and the third term?
c) \({ S }_{ n }=\frac { n }{ 2 } \left( { U }_{ 1 }+{ U }_{ n} \right) \)
Full Solution
Print from here


Three consecutive terms of an arithmetic sequence are \(x-3 \ , \ 12 \ ,\ 3x-5\)
Find \(x\)
Hint
d = U2 - U1
d = U3 - U2
Full Solution
Print from here


The 2nd term of an arithmetic sequence is 19 and the 5th term is 37.
a) Find the 10th term
b) The sum of the first n terms of this sequence exceeds 1000. Find the least value of n
Hint
a) Find d by considering how many differences there are between the 2nd and 5th terms
Full Solution
Print from here


Find the sum of all the integers between 100 and 1000 that are divisible by 9
Hint
The challenge is to recognise that this is a question that requires finding the sum of an arithmetic series.
What is the first integer after 100 that is divisible by 9?
What is the last integer before 1000 that is divisible by 9?
Full Solution
Print from here


An arithmetic sequence has first term U1 and common difference d. The sum of the first 17 terms is 136.
a) Show that \(U_1+8d=8\)
The sum of the 2nd and the 3rd terms is 42.
b) Find d.
The nth term of the sequence is Un.
c) Find the value of \(\sum _{ r=4 }^{ 17 }{ { U }_{ n } } \)
Hint
a) \(S_{ n }=\frac { n }{ 2 } (2U_{ 1 }+(n−1)d)\)
b) \(U_{ 2 }+U_{ 3 }\ =\ (U_{ 1 }+d)+(U_{ 1 }+2d)\)
c) sum of the first 17 terms - sum of the first 3 terms
Full Solution
Print from here


In an arithmetic sequence, the 9th term is 4 times the 5th term. The sum of the first 2 terms is -13.
Find the 10th term
Hint
Set up and solve two simultaneous equations using the information given:
U9 = 4U5 and S2 = -13
There is no need to use the full formula for the information about the sum since S2 = U1 + U2
Full Solution
Print from here


The first terms of a sequence are log3 x , log3 x2 , log3 x3 , ...
Find x if the sum of the first 9 terms is 135
Hint
- The terms in this sequence are arithmetic.
- This question requires good knowledge of the laws of logarithms
logc a + logc b = logc ab
logc a - logc b = logc \(\frac{a}{b}\)
- You should be able to find an expression fo rthe common difference and then use this
Full Solution
Print from here


The nth term of a geometric sequence is Un , where Un =\(48(\frac{1}{4})^n\)
a) Find U1
b) Find the sum to infinity of the series
Hint
a) let n = 1
b) \({ S }_{ \infty }=\frac { { U }_{ 1 } }{ 1-r } \)
Full Solution
Print from here


The first term of a geometric series is 10. The sum to infinity is 50.
a) Find the common ratio
The nth term is Un
b) Find the value of \(\sum _{ n=1 }^{ 20 }{ { U }_{ n } } \)
Hint
a) \({ S }_{ \infty }=\frac { { U }_{ 1 } }{ 1-r } \)
b) You can use your graphical calculator to find the sum
Full Solution
Print from here


Three terms of a geometric sequence are \(x+6 \ , \ 12 \ ,\ x-1\)
Find the possible values of x
Hint
Full Solution
Print from here


Consider the geometric sequence where the first term is 45 and the second term is 36.
a) Find the least value of n such that the nth term of the sequence is less than 1
b) Find the least value of n such that the sum of the first n terms of the sequence is more than 200.
c) Find the sum to infinity.
Hint
You can make good use of your calculator to solve the inequalties in part a and b.
Full Solution
Print from here


The sum to infinity of a geometric series is 27.
The sum of the first 3 terms is 19.
Find the common ratio
Hint
We need to solve simultaneous equations.
Notice that \(\frac { { U }_{ 1 } }{ 1-r } \) is common to both equations
Full Solution
Print from here


The 2nd, 3rd and 6th terms of an arithmetic sequence with common difference \(d, \ d\neq 0\) form the first three terms of a geometric sequence, with common ratio, r.
The 1st term of the arithmetic sequence is -2.
a) Find d.
The sum of the first n terms of the geometric sequence exceeds the sum of the first n terms of the arithmetic sequence by at least 1000.
b) Find the least value of n for which this occurs.
Hint
a) Geometric sequence is U2 , U3 , U6
b) You can make good use of the table function on your graphical calculator to solve
(sum to n terms of geometric sequence) - (sum to n terms of arithmetic sequence) > 1000
Full Solution
Print from here


U1 = cosx ,U2 = sin2x are the first two terms of a geometric sequence, \(-\frac{\pi}{2}<x<\frac{\pi}{2}\)
a) Find U3 in terms of cosx
b) Find the set of values of x for which the geometric series converges
Hint
a) \(sin2x\equiv 2sinxcosx\)
b) For a series to converge -1 < r < 1
Full Solution
Print from here


a) Jessica takes out a loan of $200 000 to buy an appartment. The interest rate is 4% and is calculated at the end of each year. Calculate to the nearest dollar the amount Jessica would owe the bank after 15 years.
b) In order to pay of the loan, she pays $P into a bank at the end of each year. She receives an interest rate of 2.5% per year. Find the amount saved after 15 years.
c) What must be the value of P so that she has saved enough money to pay off the loan.
Hint
a) This is a geometric sequence
b) This is a geometric series
c) In order to pay of the loan
Amount of savings = Amount of loan
Full Solution
Print from here


Find the value of each of the following, giving your answer as an integer
a. \({ log }_{ 4 }16\)
b. \({ log }_{ 4 }2+{ log }_{ 4 }32\)
c. \({ log }_{ 4 }8-{ log }_{ 4 }32\)
Hint
The log laws are useful
Full Solution
Print from here


a. Given that 3a =27 , write down the value of a
b. Hence of otherwise solve 27x+4 = 93x+1
Hint
Full Solution
Print from here


Solve the equation log2(x - 3) = 1 - log2(x - 4)
Hint
Rearrange the equation to have the logs on one side.
You will need to solve a quadratic equation.
Full Solution
Print from here


Solve the equation \(3^{ x-1 }=\frac { 2 }{ { 4 }^{ x+1 } } \) , giving your answer in the form \(x=\frac{lna}{lnb}\) , where a and b are rational numbers.
Hint
Take logs (base e) of both sides.
Full Solution
Print from here


Solve \(ln(sinx)−ln(cosx)=e\) for \(0<x<2\pi\)
Hint
In this question, you have to solve a trigonometric equation.
This identity is useful \(tanx = \frac{sinx}{cosx}\)
Full Solution
Print from here


\(a=\log _{ 2 }{ 2+\log _{ 2 }{ \frac { 3 }{ 2 } + } } \log _{ 2 }{ \frac { 4 }{ 3 } + } \quad ...\quad +\log _{ 2 }{ \frac { 32 }{ 31 } } \)
Given that \(a\in \mathbb{Z}\) , find the value of a
Hint
Full Solution
Print from here


The first three terms of a geometric sequence are \(\log _{ 3 }{x\quad ,\quad \log _{ 9 }{ x\quad ,\quad \log _{ 81 }{ x } } } \)
Find the value of x if the sum to infinity is 8.
Hint
The change of base formula is useful \(\log _{ b }{ a } =\frac { \log _{ c }{ a } }{ \log _{ c }{ b } } \)
Full Solution
Print from here


The values of the third row of Pascal's triangle are given below

a) Write down the values in the fourth row of Pascal's triangle
b) Hence or otherwise, find the term in x² in the expansion of \((3x+2)^4\)
Hint
Full Solution
Print from here


a) Expand (x - 3)4 and simplify your result
b) Hence find the x3 term in (x - 2)(x - 3)4 .
Hint
Full Solution
Print from here


Find the term independent of x in the expansion \((2x- \frac{3}{x^2})^6\)
Hint
The term independent of x is the term without x in it.
Remember these powers should add up to 6.
Full Solution
Print from here


The x term in the expansion \((4+2x)^3(2+ax)^4\) is -4608x
Find a
Hint
There is no need to expand\((4+2x)^3(2+ax)^4\) completely!
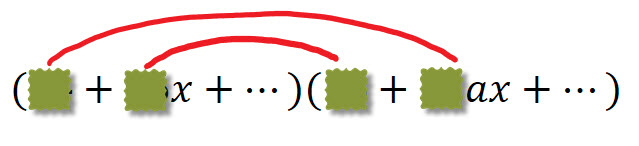
Full Solution
Print from here


\(\large(\textbf{a}+2x)^3(4-x)^4 = 6912 + \textbf{b}x +...\)
Find a and b
Hint
There is no need to expand completely \((\textbf{a}+2x)^3(4-x)^4\)

Full Solution
Print from here


a) Verify that \(x^2\left(x+1\right)^2-\left(x-1\right)^2x^2=4x^3 \) for x = 3
b) Prove that \(x^2\left(x+1\right)^2-\left(x-1\right)^2x^2\equiv4x^3 \) for all x
Hint
Full Solution
Print from here


a) Verify that \(\frac{1}{x^2}-\frac{1}{\left(x+1\right)^2}=\frac{2x+1}{x^2\left(x+1\right)^2} \) for x = -2
b) Prove that \(\frac{1}{x^2}-\frac{1}{\left(x+1\right)^2}\equiv\frac{2x+1}{x^2\left(x+1\right)^2} \) for all x
Hint
Full Solution
Print from here


Prove that the sum of three consecutive integers is divisible by 3
Hint
Let the first integer be n
Full Solution
Print from here


a) Verify that x² - 4x + 5 is positive for x = -1
b) Prove that x² - 4x + 5 is positive for all x
Hint
Full Solution
Print from here


Prove that the difference between the square of any two consecutive odd integers is divisible by 8
Hint
An odd number can be written as 2n - 1.
A number is divisible by 8 if it has a factor of 8
Full Solution
Print from here

a) Verify that \(^3 C_1\ +\ ^3 C_2\ =\ ^4C_2\)
b) Prove that \(^{n-1} C_{r-1}\ +\ ^{n-1} C_r\ =\ ^nC_r\)
Hint
\(^nC_r=\frac{n!}{(n-r)!r!}\)
Some careful manipulation is required for this proof. Consider that \(r!=r\cdot(r-1)!\)
Full Solution
Print from here
How much of Algebra Examination Questions SL have you understood?
Feedback
Which of the following best describes your feedback?




 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn