 There is quite a lot of varied content here. Most of it links to, and develops ideas of, models that we encountered in the covalent bonding and covalent structure sections (4.2 and 4.3) of the course, but also to the atomic structure; electron configuration section (2.2). It is worth ensuring that you are comfortable with the content in those sections before you begin your revision of this part of the course.
There is quite a lot of varied content here. Most of it links to, and develops ideas of, models that we encountered in the covalent bonding and covalent structure sections (4.2 and 4.3) of the course, but also to the atomic structure; electron configuration section (2.2). It is worth ensuring that you are comfortable with the content in those sections before you begin your revision of this part of the course.
Ensure you are confident using the terms below and learn the asterisked* definitions
a sigma (σ) bond*, a pi (π) bond*, VSEPR theory*, formal charge, valence electrons, expanded octet, resonance structures, delocalised electrons, conjugated system.
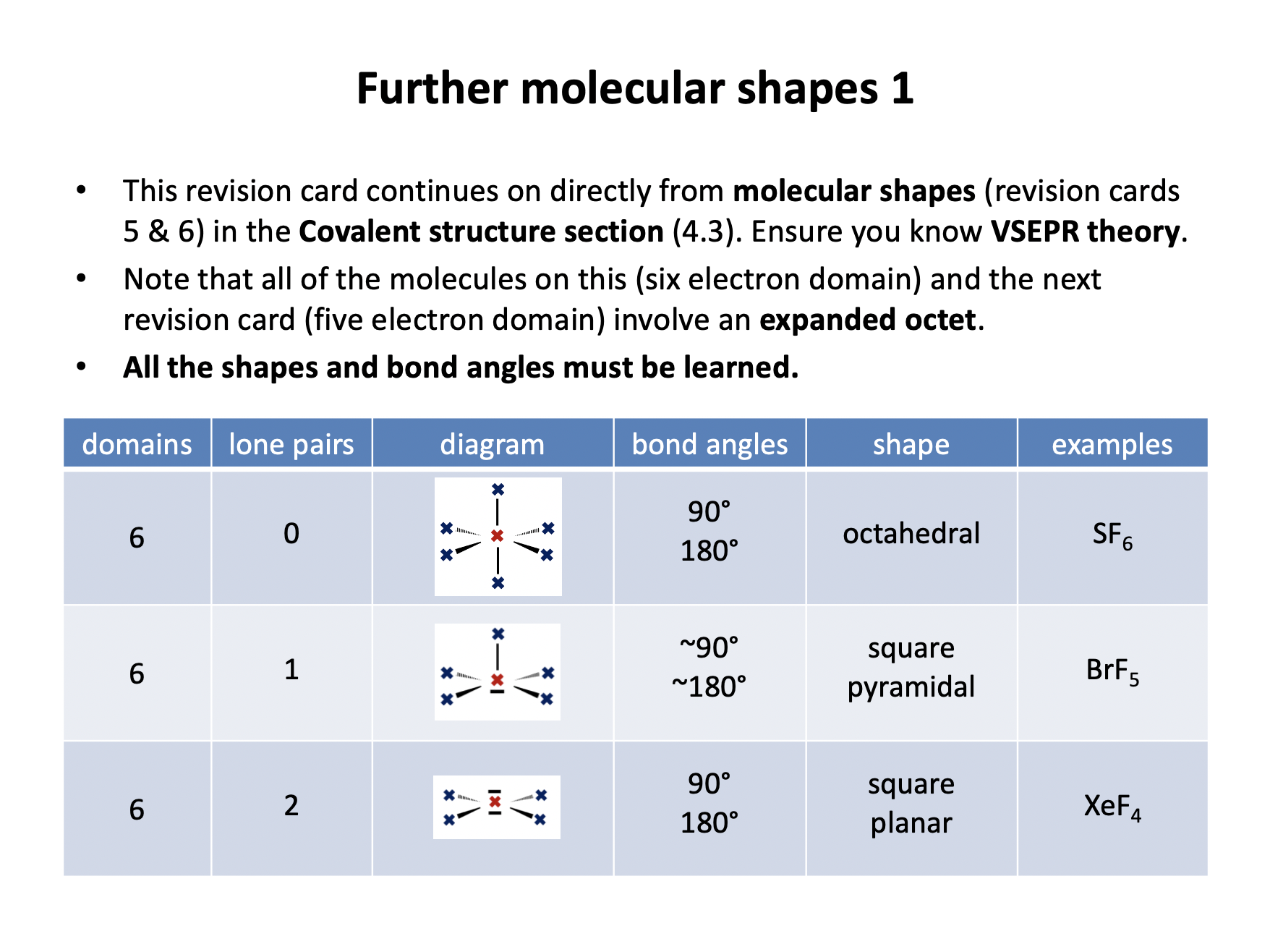
Draw a Lewis (dot-cross) diagram for sulfur hexafluoride (SF6).
What is the shape around the central atom and what are the likely bond angles?
Sulfur hexafluoride is octahedral in shape, with bond angles of 90° and 180°. The name 'octahedral' comes from the number of faces of the shape (rather than the number of vertices/corners). As you may be able to see from the diagram below, the shape is two square-based pyramids base-to-base on top of each other making an octahedron.

.png)
Draw a Lewis (dot-cross) diagram for xenon tetrafluoride (XeF4).
What is the shape around the central atom and what are the likely bond angles?
Xenon tetrafluoride is square planar in shape, with bond angles of 90° and 180°.
The shape of the electron domains is octahedral, but with two vertices missing (the lone pairs) the bonds form the shape of a square. Imagine the octahedron shown below without the top and bottom vertices.

.png)
Draw a Lewis (dot-cross) diagram for sulfur tetrafluoride (SF4).
What is the shape around the central atom and what are the likely bond angles?
Sulfur tetrafluoride is seesaw (sawhorse) in shape, with bond angles of 90°, 120° and 180°.
The shape of the electron domains is trigonal bi-pyramidal, but with one equatorial (rather than axial) vertex missing (the lone pair) the bonds form the shape of a seesaw. Imagine the shape shown below with one equatorial vertex missing.

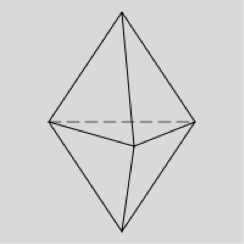
Draw a Lewis (dot-cross) diagram for iodine trifluoride (IF3).
What is the shape around the central atom and what are the likely bond angles?
Iodine trifluoride is T–shaped, with bond angles of 90° and 180°.
The shape of the electron domains is trigonal bi-pyramidal, but with two equatorial (rather than axial) vertices missing (the lone pairs) the bonds form the shape of a 'T'. Imagine the shape shown below with two equatorial vertices missing.
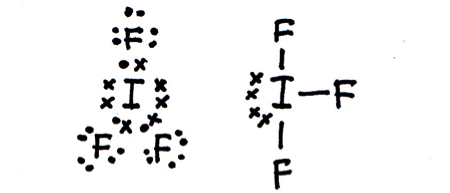

Which of the following describe/s a sigma (σ) bond?
1: The bond is formed by the end-to-end overlap of two atomic orbitals.
2: The electrons in the bond lie mostly above and below the plane of the inter-nuclear axis.
3: A sigma bond consists of two electrons .
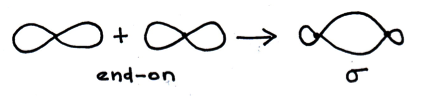
Which of the following describe/s a pi (π) bond?
1: The bond is formed by the end-to-end overlap of two atomic orbitals.
2: The electrons in the bond lie mostly above and below the plane of the inter-nuclear axis.
3: A pi bond consists of two electrons .
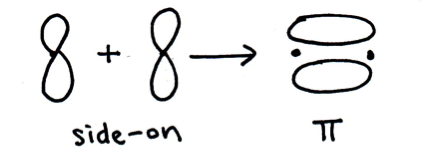
How many sigma (σ) and pi (π) bonds in total are there in ethyne (H–C≡C–H)?
Every bond in the diagram is one pair of electrons. Every sigma bond and every pi bond is one pair of electrons, so there must be a total of 5 bonds.
A single bond is just a sigma bond.
A double bond is one sigma bond and one pi bond.
A triple bond is one sigma and two pi bonds.
There are therefore 3 sigma bonds and 2 pi bonds present in ethyne.
When the bonding in a chemical species cannot be adequately represented by one single Lewis diagram, resonance structures may be used. When the resonance structures for a molecule of ozone, O3, are drawn, what are the formal charges on each of the oxygen atoms?
Formal charge = normal valence electrons – (non-bonding electrons + (½ × bonding electrons))
This can be confusing (and appear in different formats): formal charge works out the number of electrons an atom 'has' compared to how many it 'should have'.
The normal valence electrons is equal to the number of electrons in an atom's valence shell when in a 'normal' (ground or isolated) state. E.g oxygen in group VI (16) has 6 electrons in its valence shell.
(non-bonding electrons + (½ × bonding electrons)) are the electrons that the atom actually has in its current state.
The electrons an atom 'has' (all of the non-bonding electrons and half of the bonding electrons are 'owned' by that atom) are being taken away from the electrons it 'should have'. Atoms that have a formal charge of zero are in a 'normal' (electronically stable) state those that have a +ve formal charge are electron deficient; –ve, electron rich.
The oxygen atoms have FC of (left-to-right first resonance structure below):
FC = 6 – (4 + (½ × 4)) = 6 – (6) = 0
FC = 6 – (2 + (½ × 6)) = 6 – (5) = +1
FC = 6 – (6 + (½ × 2)) = 6 – (7) = –1
(or vica versa) respectively.


Sulfur dioxide can be represented by several different Lewis diagrams, two of which are shown below:
.png)
| Lewis diagram A | Lewis Diagram B |
What are the formal charges (FC) on each of the sulfur atoms in diagram A and B respectively, and which Lewis diagram is the most electronically stable representation of SO2?
The atoms of Lewis diagram A have FC of:
Sulfur FC = 6 – (2 + (½ × 8)) = 6 – (6) = 0
Oxygen (both the same) FC = 6 – (4 + (½ × 4)) = 6 – (6) = 0
The atoms of Lewis diagram B have FC of:
Sulfur FC = 6 – (2 + (½ × 6)) = 6 – (5) = +1
Oxygen (double bonded) FC = 6 – (4 + (½ × 4)) = 6 – (6) = 0
Oxygen (single bonded) FC = 6 – (6 + (½ × 2)) = 6 – (7) = –1
The first Lewis diagram, A, (in which the sulfur has expanded its octet) is therefore the most stable since all atoms in the structure have FC of zero.
'FC 0 (sulfur A); FC +1 (sulfur B); most stable diagram is A' is the correct answer.
Remember:
Formal charge = normal valence electrons – (non-bonding electrons + (½ × bonding electrons))
This can be confusing (and appear in different formats): formal charge works out the number of electrons an atom 'has' compared to how many it 'should have'.
The normal valence electrons is equal to the number of electrons in an atom's valence shell when in a 'normal' (ground or isolated) state. E.g sulfur in group VI (16) has 6 electrons in its valence shell.
(non-bonding electrons + (½ × bonding electrons)) are the electrons that the atom actually has in its current state.
The electrons an atom 'has' (all of the non-bonding electrons and half of the bonding electrons are 'owned' by that atom) are being taken away from the electrons it 'should have'. Atoms that have a formal charge of zero are in a 'normal' (electronically stable) state those that have a +ve formal charge are electron deficient; –ve, electron rich.
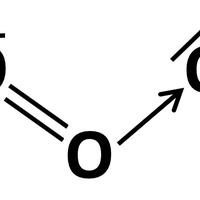
Oxygen molecules can be broken up into oxygen atoms:
O2 → 2O
And oxygen atoms can then react with oxygen molecules to form ozone:
O2 + O → O3
Ozone can also dissociate back to an oxygen molecule and an oxygen atom :
O3 → O2 + O
Light from which region of the electromagnetic spectrum is required to dissociate oxygen and to dissociate ozone respectively?
Ultra-violet light is needed to dissociate both oxygen and ozone. The wavelength of light needed to dissociate oxygen is lower (the light is therefore higher in energy) than ozone. This is because the double bond in oxygen is stronger than the '1½' bonds in ozone (normally shown with the resonance structures as alternating double/single bonds).

Chlorofluorocarbons (CFCs) and oxides of nitrogen, NOx can catalyse the decomposition of ozone in the upper atmosphere.
Possible two-step mechanisms are given below for a chlorine radical (from CFCs) and for NO:
| O3 + Cl → ClO + O2 | O3 + NO → NO2 + O2 |
| ClO + O3 → Cl + 2O2 | NO2 + O3 → NO + 2O2 |
How many ozone molecules can one mole of chlorine radicals, and one mole of nitrogen monoxide molecules respectively, decompose?
The chlorine radicals and nitrogen monoxide are both acting as catalysts in these reactions. Thus, despite the mechanisms both showing a 1:2 molar ratio overall of catalyst to ozone molecules, both catalysts are re-produced at the end of the reaction, and are not 'used up', so they can go on decomposing many thousands of ozone molecules before they come to the end of their lifetimes.
Calculator question: Given that the bond energy of an O=O bond is 498 kJ mol–1, calculate the wavelength of light (in metres) required to break a single O=O bond.
Use E = hν and \(c = νλ\) from the data book.
E = hν (energy = Planck constant × frequency) is given in the data book.
Also in the data book is \(c = νλ\) (speed of light = frequency × wavelength)
Rearrangement of \(c = νλ\) will give \(ν = {c \over λ}\) (frequency = speed of light / wavelength).
So using E = hν and \(ν = {c \over λ}\) by substituting frequency from the second expression into the first expression gives \(E = {hc \over λ}\).
Energy is given for one mole of electrons in the question, so 498 kJ mol–1 must be divided by Avogadro's number (L) to give the value for one bond.
498/6.02×1023=8.27...×10−22 kJ which is 8.27...×10−19 J (must be in Joules as Planck's constant is in Joule seconds, Js)
Thus, putting in all the known values, \(E = {hc \over λ}\) becomes:
\({8.2724252×10^{-19}} = {(6.63×10^{-34})(3.00×10^{8}) \over λ}\)
Rearranging:
\({λ} = {(6.63×10^{-34})(3.00×10^{8}) \over 8.2724252×10^{-19}}\)
Wavelength is therefore: 2.40×10−7 m (240nm)
Paper 1
Core (SL&HL): Bonding and Structure core (SL and HL) paper 1 questions
AHL (HL only): Bonding and Structure AHL (HL only) paper 1 questions
Paper 2
Core (SL&HL): Bonding & Structure core (SL & HL) paper 2 questions
AHL (HL only): Bonding & Structure AHL (HL only) paper 2 questions
How much of Further covalent bonding and structure have you understood?
























 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn