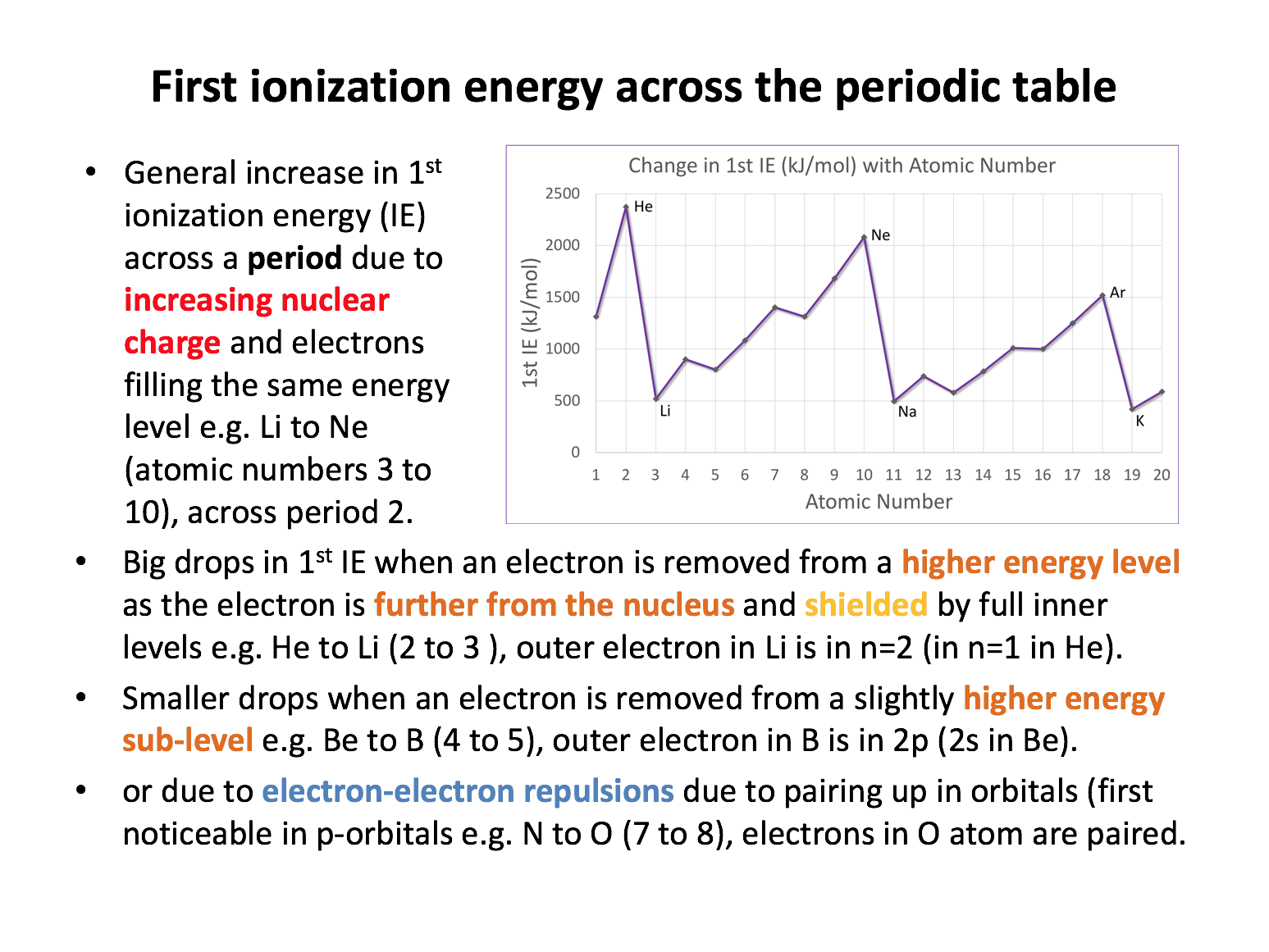
 First ionisation energies provide evidence for our quantum mechanical model of the atom.
First ionisation energies provide evidence for our quantum mechanical model of the atom.
This is a challenging section of the course; abstract concepts and lots of specific terms, combined later with mathematics create many opportunities for mistakes in your answers! Be reassured, however, that although the content is difficult, there are only so many ways in which questions can be presented. Tough content, but not pages of information to learn.
The language here is very important, using the specific terms (e.g. orbital, sub-level etc.) correctly will get you the marks in the exams. Errors in language are very common in this part of the course, so learn the vocabulary thoroughly using the flash cards.
Ensure that you can sketch the first ionisation energy graph shown on revision card 3, and practise explaining it (to yourself or even better to someone else who also needs to learn it - take it in turns). In time it will stick, and from the understanding of this graph, you will be able to 'extrapolate' your knowledge to other problems/data.
The calculation of the first ionisation energy of hydrogen is particularly tough to get your head around. Using revision card 6 as your model, practise writing out the calculation repeatedly, and explaining it as you go. When you know it 'by wrote', you will also be able to more easily apply your knowledge to slight variations on the problem.
Ensure you are confident using the terms below and learn the asterisked* definitions
energy level, sub-level, orbital, atomic radius, nuclear charge, shielding*, first ionization energy*, second ionization energy*, convergence limit
What is the correct electronic configuration for the germanium ion Ge4+?
The electronic configuration for the germanium atom is 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p2, but the 4+ ion has lost 4 electrons. They are lost from the highest energy sublevels first; that is the 4p and then the 4s (4s is filled first and lost first) - as the 3d level slips below the 4s level in energy when the 3d level has electrons in it. So the answer is 1s2 2s2 2p6 3s2 3p6 4s0 3d10 4p0.
In the hydrogen atomic absorbtion spectrum, the limit of convergence at high frequency corresponds to an electron transition between which of the following energy levels?
The question refers to an absorbtion spectrum, so the transtion will be from a lower to higher energy level. The convergence limit in the hydrogen atomic absorbtion spectrum indicates the point of ionisation; the electron is no longer part of the hydrogen atom. This is the transition from n=1 (the ground state for hydrogen) to n=∞ (infinity).
Which of the following contribute to sulfur (1000 kJmol−1) having a lower first ionisation energy than phosphorus (1012 kJmol−1), even though sulfur has a higher nuclear charge than phosphorus?
1 The electron removed is in a higher energy level, with less attraction to the nucleus
2 The electron removed is paired-up with another electron in the same orbital, resulting in repulsion
3 The electron removed has greater 'shielding' (repulsion) by complete inner energy levels of electrons
The electron removed from sulfur is removed from the 3p sub-level. The electron removed from phosphorus is also in the 3p sub-level. Thus explanations 1 and 3 do not contribute. Sulfur's outer electron is however, paired-up, unlike the electrons of phosphorus which occupy orbitals singly (on their own) so explanation 2 does apply.
Which of the following contribute to sodium (496 kJmol−1) having a lower first ionisation energy than neon (2081 kJmol−1), even though sodium has a higher nuclear charge than neon?
1 The electron removed is in a higher energy level, with less attraction to the nucleus
2 The electron removed is paired-up with another electron in the same orbital, resulting in repulsion
3 The electron removed has greater 'shielding' (repulsion) by complete inner energy levels of electrons
The electron removed from sodium is removed from the 3s sub-level. The electron removed from neon is from the 2p sub-level. Explanations 1 and 3 both contribute to the ionisation energy of sodium being lower than neon; the 3s sub-level is in the n=3 energy level further from the nucleus with less nuclear attraction and the complete n=2 level of electrons will shield (repel) the outer electron to a greater extent (than in neon). Sodium's outer electron in 3s is, however, not paired-up, so explanation 2 does not apply.
The first four successive ionisation energies (kJ mol−1) for an element, Z, are 419, 3052, 4420, 5877. Which one of the following is most likely to be the electronic configuration for element Z?
The largest jump in ionisation energies (IE) here is between the removal of the first and second electrons. The difference of approximately 2500 kJ mol−1 is larger than the other differences. In the configuration 1s2 2s2 2p6 the first 4 electrons removed are all in the 2p sub-level, so there will be no large jumps in IE.
The configuration 1s2 2s2 2p6 3s2 3p1 would result in a noticably larger jump between the first and second IE (3p to 3s), but would also have an even more significant jump between the third and fourth IEs (3s to 2p).
The configuration 1s2 2s2 2p6 3s2 3p6 4s2 would result in the largest jump after the second IE.
The configuration 1s2 2s2 2p6 3s2 3p6 4s1 is the correct answer - resulting in the largest jump in IE between the removal of the first and second electrons.
The first four successive ionisation energies (kJ mol−1) for an element, Z, are 900, 1757, 14849, 21007. Which one of the following elements is most likely to be element Z?
The largest jump in ionisation energies (IE) here is between the removal of the second and third electrons. The difference of approximately 13000 kJ mol−1 is huge and indicates that the electron is being removed from a (much) lower energy level.
Oxygen's first 4 electrons are in the 2p sub-level, so there will be no large jumps in IE. Both carbon and silicon's first 2 electrons will be removed first from a p sub-level, with the third electron removed from an s sub-level; a small jump in IE might be apparent. But the jump here is very dramatic and indicates that Beryllium is the correct answer; the first 2 electrons will be removed from the 2s sub-level, the third and fourth from the 1s (far lower in energy with strong nuclear attraction and no shielding makes the electrons very difficult to remove).
The first four successive ionisation energies for three elements are given below. Match the three elements oxygen, silicon and phosphorus to the correct series of values (kJ mol−1) .
1: 1012, 1907, 2914, 4964
2: 1314, 3388, 5301, 7469
3: 787, 1577, 3232, 4356
The electron configurations for the three elements are; oxygen 1s2 2s2 2p4 ; silicon 1s2 2s2 2p6 3s2 3p2 ; phosphorus 1s2 2s2 2p6 3s2 3p3.
For oxygen there will be no large jumps in ionisation energy, since the first four electrons are all removed from the 2p sub-level, so the match for oxygen is series 2, with a similar difference of approx. 2000 units between each IE.
For silicon the largest jump with be between the second and third IEs (3p to 3s), so the match for silicon is series 3, with the largest difference of approx. 1700 units between the second and third IEs.
For phosphorus the largest jump with be between the third and fourth IEs (3p to 3s), so the match for phosphorus is series 1, with the largest difference of approx. 2000 units between the third and fourth IEs.
Which of the following states a correct relationship involving one or more of energy (E), frequency (ν) and wavelength (λ) of light, where h is the Planck constant and c is the speed of light (in a vacuum)?
E = hν (energy = Planck constant × frequency) and \(ν = {c \over λ}\)(frequency = speed of light / wavelength).
Substituting frequency from the second expression into the first expression gives \(E = {hc \over λ}\), which is therefore the correct answer.
Energy and frequency are both proportional to 1 / wavelength but not equal to. \(λ = ν\) is incorrect, the relationship between wavelength and frequency is given above.
Which shows the correct equation for the calculation of the energy of one mole of photons of yellow light with wavelength 580nm?
E = hν (energy = Planck constant × frequency) and \(ν = {c \over λ}\)(frequency = speed of light / wavelength).
Substituting frequency from the second expression into the first expression gives \(E = {hc \over λ}\).
580nm is 5.80×10−7m (wavelength must be in metres) and the energy is for one mole of photons so \(E = {hc \over λ}\)must be multiplied by Avogadro's constant (6.02×1023) .
Thus \(E = {(6.02×10^{23})(6.63×10^{-34})(3.00×10^{8}) \over 5.80×10^{-7}}\) is the correct answer.
Paper 1
Core (SL&HL): Atomic Structure core (SL and HL) paper 1 questions
AHL (HL only): Atomic Structure AHL (HL only) paper 1 questions
Paper 2
Core (SL&HL): Atomic Structure core (SL & HL) paper 2 questions
AHL (HL only): Atomic Structure AHL (HL only) paper 2 questions
How much of Electrons in atoms have you understood?













 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn