3.10 Vector Equations of Lines

1 2a 2b 3a 3b 4 5a 5b 5c 6a 6b 7a 7b 7c 8a 8b 9a 9b

Question 1

Marks: 7

The line $l$ has equation $r = (\begin{matrix} 4 \\ 0 \\ 3 \end{matrix}) + λ (\begin{matrix} - 1 \\ - 2 \\ 5 \end{matrix})$ and point A has coordinates $(3, t, 2)$ . Given that the shortest distance between point A and the line is $\frac{\sqrt{645}}{15}$ units, find $t$ , where $t \in ℤ$ .

Key Concepts

Equation of a Line in Vector Form
Shortest Distance Between a Point and a Line

Question 2a

Marks: 6

A line $l_{1}$ has the equation $r_{1} = (2 + λ) i + (6 λ - 3) j + (5 + 2 λ) k$ and intersects the line $l_{2}$ with equation $r_{2} = 5 i + (7 - 4 μ) j + (- 3 - 7 μ) k$ at point P, when $λ = 3$ .

A third line $l_{3}$ runs parallel to $l_{1}$ and also intersects $l_{2}$ at point $X (t, t - 2, - 2 t)$ .

(a)

Find the parametric equations of

l_{3}

Key Concepts

Coincident, Parallel, Intersecting & Skew Lines
Equation of a Line in Parametric Form

Question 2b

Marks: 2

(b)

Find the distance

|PX|

Key Concepts

Magnitude of a Vector

Question 3a

Marks: 4

Consider the two intersecting lines $l_{1}$ and $l_{2}$ defined by the equations:

$l_{1} : r = (\begin{matrix} 9 \\ 18 \\ 11 \end{matrix}) + λ (\begin{matrix} - 6 \\ - 3 \\ k \end{matrix})$

$l_{2} : \frac{x + 5}{2} = \frac{y + t}{- 4} = \frac{z - 20}{3}$

(a)

Given that the angle between

l_{1}

and

l_{2}

1.281

rad, correct to 4 significant figures, find the value of

k

, where

k \in ℤ

Key Concepts

Angle Between Two Lines

Question 3b

Marks: 3

(b)

Find the value of

t

, giving your answer correct to 3 significant figures.

Key Concepts

Coincident, Parallel, Intersecting & Skew Lines

Question 4

Marks: 8

Consider the two lines $l_{1}$ and $l_{2}$ , where $l_{1}$ passes through the points $A (11, - 2, 3)$ and $B (4, 4, - 5)$ and $l_{2}$ is defined by the Cartesian equations $\frac{x + 7}{3} = \frac{2 y + 9}{6} = \frac{z + 4}{- 4}$

Find the shortest distance between the two lines.

Key Concepts

Equation of a Line in Cartesian Form
Shortest Distance Between Two Lines

Question 5a

Marks: 6

Consider the line $l_{1}$ as defined by the equation $r_{1} = (\begin{matrix} - 2 \\ 5 \\ - 8 \end{matrix}) + α (\begin{matrix} 2 \\ - 1 \\ 3 \end{matrix})$ .

A point $P (r, t, - r)$ lies at a distance of $\sqrt{405}$ units perpendicular from a point $X (17, 15, - 8)$ on $l_{1}$ .

(a)

Find all possible coordinates of

P

Key Concepts

Perpendicular Vectors
Magnitude of a Vector

Question 5b

Marks: 2

(b)

Given that

t > 0

, write down the set of parametric equations that defines the line

l_{2}

that passes through points

P

and

X

Key Concepts

Equation of a Line in Parametric Form

Question 5c

Marks: 3

A third line $l_{3}$ is defined by the equations $\frac{- x - 13}{5} = \frac{- y - 9}{4} = \frac{z - 4}{2}$ .

(c)

Determine the relationship between lines

l_{2}

and

l_{3}

Key Concepts

Coincident, Parallel, Intersecting & Skew Lines

Question 6a

Marks: 2

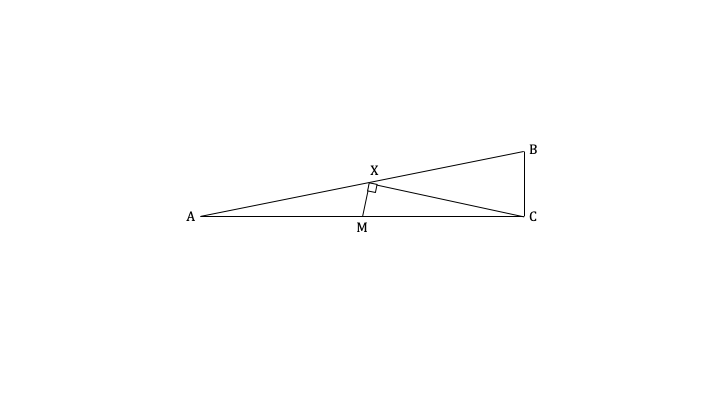
A wheelchair ramp is required to provide access to a building with a door that is located 22 cm above ground level. The maximum angle that a ramp must be from the horizontal is 4.8°.

(a)

Calculate the minimum horizontal distance that the ramp must extend out.

Key Concepts

Right-Angled Trigonometry

Question 6b

Marks: 8

The wheelchair ramp is supported by a steel frame. A cross section of the ramp can be seen in the diagram below. A metal strut joins M, the midpoint of [AC], to a point X on the line [AB]. [AB].XM=11.1 cm and $M \hat{X} C$ =90°.

q6a_3-10_vector-equations-of-lines_very-hard_ib_aa_hl_maths-diagram

(b)

Using the horizontal distance found in part (a) and assuming that point A is at the origin, use a vector method to calculate the length XB.

Key Concepts

Perpendicular Vectors

Question 7a

Marks: 2

Two drones X and Y are being flown over an area of rainforest to look for signs of illegal logging. Their positions relative to the observation centre, are given by

$r_{x} = (\begin{matrix} - 3 \\ 1.6 \\ 2.5 \end{matrix}) + t (\begin{matrix} 2 \\ - 2 \\ 1 \end{matrix})$ and $r_{y} = (\begin{matrix} 2.5 \\ 0 \\ - 2 \end{matrix}) + t (\begin{matrix} 1.5 \\ 6 \\ 4 \end{matrix})$

at time $t$ minutes after take-off, $0 \leq t < 20$ . All distances are in metres.

(a)

Verify that the two drones will not collide.

Key Concepts

Coincident, Parallel, Intersecting & Skew Lines

Question 7b

Marks: 6

(b)

Find the shortest distance between the two drones and the time at which it occurs.

Key Concepts

Basic Coordinate Geometry
Modelling with Differentiation

Question 7c

Marks: 6

A third drone Z begins its flight at $t = 8$ and its position relative to the observation centre is given by $r_{z} = (\begin{matrix} 2 \\ 1.5 \\ 4.5 \end{matrix}) + t (\begin{matrix} 3 \\ 4 \\ 1 \end{matrix})$

Each drone can observe a circular area of ground, $A,$ such that $A = 1.8 h^{2}$ where $h$ is the height of the drone above the ground in metres.

(c)

Show that the area of ground that can be observed by drone Z five minutes after it takes off overlaps with the area of ground that can be observed by drone Y at that time.

Key Concepts

Equation of a Line in Vector Form
Magnitude of a Vector

Question 8a

Marks: 5

Consider the tetrahedron ABCD, where A(3, 5, 8), B(-2, 3, 2), C(5, -1, 3) and D(-3, 0, 1). M is the midpoint of the line BC and point P lies along the line DM.

(a)

Given that the volume of the tetrahedron ABCP is

\frac{1}{3}

of the volume of the tetrahedron ABCD, find the Cartesian equations of the line going through points A and P.

Key Concepts

Displacement Vectors
Equation of a Line in Cartesian Form

Question 8b

Marks: 5

(b) X is the midpoint of [AD].

Find the coordinates of the point of intersection between the line found in part (a) and the line going through [MX].

Key Concepts

Coincident, Parallel, Intersecting & Skew Lines

Question 9a

Marks: 6

A car is moving at a constant speed of 15 ms^-1 in the direction parallel to the vector $3 i - 6 j .$ Two birds are perched at points $A (17, 28, 16)$ and $B (- 48, 128, 26)$ .

At $t = 0$ , the car is located at $(2, 4, 0)$ and the bird at point A starts to fly at a constant velocity of $\frac{7 \sqrt{365}}{10}$ ms^-1. The bird at point B begins to fly at a constant velocity in the direction of the vector $52 i - 60 j - 9 k$ when $t = 1.2$ .

When bird A reaches the position of $(44, - 24, 4)$ , both birds and the car lie in a straight line.

(a)

Find the equation of the line along which the birds and car lie.

Key Concepts

Kinematics using Vectors
Equation of a Line in Vector Form

Question 9b

Marks: 6

(b)

Find the speed at which bird B is travelling.

Key Concepts

Kinematics using Vectors

DP IB Maths: AA HL

Topic Questions

3.10 Vector Equations of Lines

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Resources

Members

Company

Quick Links