| Date | November 2017 | Marks available | 4 | Reference code | 17N.2.AHL.TZ0.H_11 |
| Level | Additional Higher Level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Sketch | Question number | H_11 | Adapted from | N/A |
Question
Consider the function .
Let .
Determine an expression for in terms of .
Sketch a graph of for .
Find the -coordinate(s) of the point(s) of inflexion of the graph of , labelling these clearly on the graph of .
Express in terms of .
Express in terms of .
Hence show that can be expressed as .
Solve the equation , giving your answers in the form where .
Markscheme
(or equivalent) (M1)A1
[2 marks]
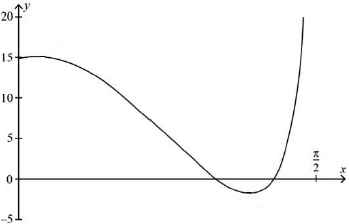 A1A1A1A1
A1A1A1A1
Note: Award A1 for correct behaviour at , A1 for correct domain and correct behaviour for , A1 for two clear intersections with -axis and minimum point, A1 for clear maximum point.
[4 marks]
A1
A1
[2 marks]
attempt to write in terms of only (M1)
A1
[2 marks]
(A1)
attempt to use (M1)
A1
[3 marks]
M1
(or equivalent) A1
AG
[2 marks]
or (M1)
A1
A1
Note: Only accept answers given the required form.
[3 marks]

