| Date | May 2022 | Marks available | 3 | Reference code | 22M.1.SL.TZ2.7 |
| Level | Standard Level | Paper | Paper 1 (without calculator) | Time zone | Time zone 2 |
| Command term | Find | Question number | 7 | Adapted from | N/A |
Question
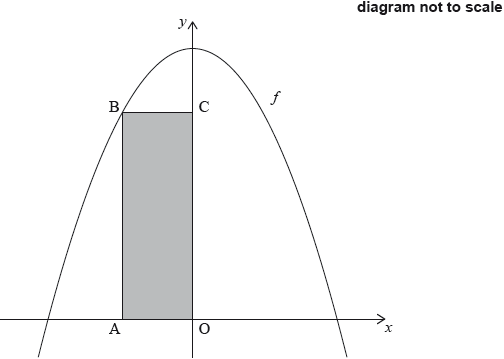
The following diagram shows part of the graph of a quadratic function .
The graph of has its vertex at , and it passes through point as shown.
The function can be written in the form .
The line is tangent to the graph of at .
Now consider another function . The derivative of is given by , where .
Write down the equation of the axis of symmetry.
Write down the values of and .
Point has coordinates . Find the value of .
Find the equation of .
Find the values of for which is an increasing function.
Find the values of for which the graph of is concave-up.
Markscheme
A1
Note: Must be an equation in the form “ ”. Do not accept or .
[1 mark]
(accept ) A1A1
[2 marks]
attempt to substitute coordinates of (M1)
A1
[2 marks]
recognize need to find derivative of (M1)
or A1
(may be seen as gradient in their equation) (A1)
or A1
Note: Award A0 for .
[4 marks]
METHOD 1
Recognizing that for to be increasing, , or (M1)
The vertex must be above the -axis, (R1)
A1
METHOD 2
attempting to find discriminant of (M1)
recognizing discriminant must be negative (R1)
OR
A1
[3 marks]
recognizing that for to be concave up, (M1)
when (R1)
A1
[3 marks]
Examiners report
In parts (a) and (b) of this question, a majority of candidates recognized the connection between the coordinates of the vertex and the axis of symmetry and the values of and , and most candidates were able to successfully substitute the coordinates of point Q to find the value of . In part (c), the candidates who recognized the need to use the derivative to find the gradient of the tangent were generally successful in finding the equation of the line, although many did not give their equation in the proper form in terms of and , and instead wrote , thus losing the final mark. Parts (d) and (e) were much more challenging for candidates. Although a good number of candidates recognized that in part (d), and in part (e), very few were able to proceed beyond this point and find the correct inequalities for their final answers.