| Date | May 2017 | Marks available | 5 | Reference code | 17M.1.AHL.TZ2.H_9 |
| Level | Additional Higher Level | Paper | Paper 1 (without calculator) | Time zone | Time zone 2 |
| Command term | Find | Question number | H_9 | Adapted from | N/A |
Question
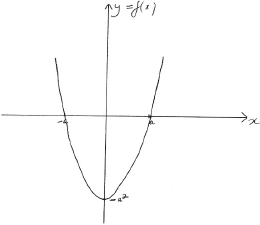
Consider the function defined by where is a positive constant.
The function is defined by for .
Showing any and intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
;
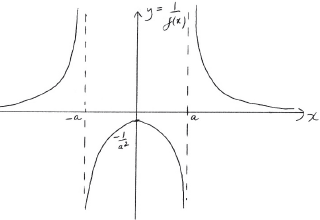
Showing any and intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
;
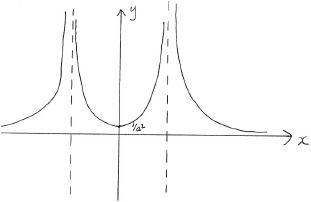
Showing any and intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
.
Find .
By finding explain why is an increasing function.
Markscheme
A1 for correct shape
A1 for correct and intercepts and minimum point
[2 marks]
A1 for correct shape
A1 for correct vertical asymptotes
A1 for correct implied horizontal asymptote
A1 for correct maximum point
[??? marks]
A1 for reflecting negative branch from (ii) in the -axis
A1 for correctly labelled minimum point
[2 marks]
EITHER
attempt at integration by parts (M1)
A1A1
A1
A1
OR
attempt at integration by parts (M1)
A1A1
A1
A1
[5 marks]
M1A1A1
Note: Method mark is for differentiating the product. Award A1 for each correct term.
both parts of the expression are positive hence is positive R1
and therefore is an increasing function (for ) AG
[4 marks]
Examiners report
Syllabus sections
-
22M.3.AHL.TZ1.2g.i:
Show that the -coordinate of is .
You are not required to demonstrate a change in concavity.
-
18M.2.SL.TZ2.S_9a:
Find the initial velocity of P.
-
18M.2.SL.TZ2.S_9d:
Find the acceleration of P when it changes direction.
-
22M.1.SL.TZ1.7e.ii:
Find the values of for which the graph of is concave-down. Justify your answer.
-
22M.1.SL.TZ1.7e.i:
Write down the value of .
-
19M.2.AHL.TZ2.H_9c:
Hence, or otherwise, state the condition on such that all roots of the equation are real.
-
18N.2.AHL.TZ0.H_9c.i:
sketch the graph of , showing clearly any axis intercepts and giving the equations of any asymptotes.
-
17M.1.AHL.TZ2.H_9a.i:
Showing any and intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
;
-
18M.1.AHL.TZ1.H_9c:
Sketch the graph of showing clearly the position of the points A and B.
-
19M.2.AHL.TZ2.H_9b:
Sketch the graph of , stating clearly the coordinates of any maximum and minimum points and intersections with axes.
-
18M.2.SL.TZ1.S_10a:
Find the coordinates of A.
-
18M.2.SL.TZ1.S_10b.i:
For the graph of , write down the amplitude.
-
19M.2.SL.TZ1.S_4a:
Sketch the graph of on the grid below:
-
18M.2.SL.TZ1.T_6c:
Find the height of the cylinder, h , of the new trash can, in terms of r.
-
19M.2.SL.TZ2.S_5c:
Find the value of for which the population of fish is increasing most rapidly.
-
18M.1.SL.TZ2.T_13a:
Find the cost of producing 70 shirts.
-
18M.1.SL.TZ2.T_13c:
Find the number of shirts produced when the cost of production is lowest.
-
18M.2.SL.TZ1.T_6b:
Find the total volume of the trash can.
-
18N.2.SL.TZ0.T_6a:
Calculate the area of cloth, in cm2, needed to make Haruka’s bag.
-
17M.1.AHL.TZ2.H_9a.ii:
Showing any and intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
;
-
19N.2.SL.TZ0.S_8d:
Let be the region enclosed by the graph of , the -axis and the lines and . The region is rotated 360º about the -axis. Find the volume of the solid formed.
-
18M.2.SL.TZ1.T_6e:
Using your graphic display calculator, find the value of r which maximizes the value of V.
-
19M.2.SL.TZ2.T_5b:
Write down the -intercept of the graph of .
-
SPM.1.SL.TZ0.8b:
Find the value of and the value of .
-
19N.2.SL.TZ0.S_8c.ii:
Find the rate of change of at .
-
17M.2.SL.TZ2.T_6f:
Write down the number of possible solutions to the equation .
-
17M.2.SL.TZ2.S_8b.i:
Write down the coordinates of A.
-
17M.2.SL.TZ2.S_8c.i:
Find the coordinates of B.
-
18M.2.SL.TZ2.S_9e:
Find the total distance travelled by P.
-
SPM.1.SL.TZ0.8c.i:
Sketch the graph of .
-
17N.2.AHL.TZ0.H_11a.i:
Determine an expression for in terms of .
-
16N.1.AHL.TZ0.H_11h:
Find the value for and comment on its meaning with respect to the shape of the graph.
-
18M.2.SL.TZ1.S_10e:
Find the first time when the ball’s speed is changing at a rate of 2 cm s−2.
-
17M.2.SL.TZ1.S_10b.i:
Find .
-
19N.1.SL.TZ0.S_8a:
Write down an expression for in terms of .
-
19N.2.SL.TZ0.S_8b.ii:
Find the equation of the tangent to the graph of at .
-
18N.1.AHL.TZ0.H_10b:
Hence, show that , .
-
21N.1.SL.TZ0.9c.ii:
Find the values of where the graph of has points of inflexion. Justify your answer.
-
19N.1.SL.TZ0.S_8d.i:
Find the value of for which is a maximum.
-
19N.2.SL.TZ0.S_8a:
Find the value of .
-
16N.1.AHL.TZ0.H_11c:
Show that the function has a local maximum value when .
-
SPM.1.SL.TZ0.8a:
Find .
-
18N.2.AHL.TZ0.H_9c.ii:
sketch the graph of , showing clearly any axis intercepts and giving the equations of any asymptotes.
-
17N.1.SL.TZ0.S_7:
Consider , for , where .
The equation has exactly one solution. Find the value of .
-
17M.2.SL.TZ2.S_8b.ii:
Write down the rate of change of at A.
-
19M.2.SL.TZ2.T_5c:
Sketch the graph of for −3 ≤ ≤ 3 and −4 ≤ ≤ 12.
-
17N.1.SL.TZ0.T_15a:
Write down how many kilograms of cheese Maria sells in one week if the price of a kilogram of cheese is 8 EUR.
-
18N.1.SL.TZ0.S_10b.i:
Find .
-
18M.2.SL.TZ1.S_10d:
Find the maximum speed of the ball.
-
18M.1.SL.TZ2.S_9b:
Show that .
-
17M.1.AHL.TZ2.H_9a.iii:
Showing any and intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
.
-
18M.2.SL.TZ2.S_9b:
Find the maximum speed of P.
-
18M.2.SL.TZ1.S_7a:
Given that xk + 1 = xk + a, find a.
-
17M.2.SL.TZ2.S_8a:
Find the value of .
-
18N.1.SL.TZ0.S_10c:
The graph of has a local minimum at the point Q. The line L passes through Q.
Find the value of .
-
18M.1.AHL.TZ1.H_9b.ii:
The coordinates of B can be expressed in the form B where a, b. Find the value of a and the value of b.
-
17N.2.AHL.TZ0.H_10b:
Sketch the graph of showing clearly the minimum point and any asymptotic behaviour.
-
19N.1.SL.TZ0.S_8b:
Find an expression for in terms of .
-
19M.2.SL.TZ1.S_4c:
Hence find the values of for which the graph of is concave-down.
-
19M.2.SL.TZ2.S_5a:
Find the population of fish at = 10.
-
19N.2.SL.TZ0.S_8b.i:
Write down the coordinates of .
-
18N.1.AHL.TZ0.H_10a:
Use integration by parts to show that , .
-
17M.2.SL.TZ2.S_8d:
Let be the region enclosed by the graph of , the -axis, the line and the line . The region is rotated 360° about the -axis. Find the volume of the solid formed.
-
22M.3.AHL.TZ1.2g.ii:
Hence describe numerically the horizontal position of point relative to the horizontal positions of the points and .
-
22M.3.AHL.TZ2.1d.ii:
Hence deduce that the curve has no local minimum or maximum points.
-
EXN.1.SL.TZ0.7c:
Find an expression for in terms of .
-
EXN.1.SL.TZ0.7e:
Determine the maximum area of rectangle .
-
22M.1.SL.TZ2.7e:
Find the values of for which the graph of is concave-up.
-
22M.1.AHL.TZ2.6b:
The range of is , where .
Find the value of and the value of .
-
SPM.1.SL.TZ0.8c.ii:
Hence explain why the graph of has a local maximum point at .
-
22M.2.AHL.TZ1.12c.iii:
Using the graph of , suggest a reason why the approximation given by Euler’s method in part (a) is not a good estimate to the actual value of at .
-
22M.2.AHL.TZ2.11e:
Let represent the distance between airplane and airplane for .
Find the minimum value of .
-
22M.2.AHL.TZ2.12d:
Hence determine the maximum value of in terms of and .
-
17N.2.AHL.TZ0.H_10a.ii:
Determine the values of for which is a decreasing function.
-
20N.2.SL.TZ0.S_10a:
Show that .
-
EXN.2.AHL.TZ0.12c:
The curve has a point of inflexion at where . Determine the coordinates of this point of inflexion.
-
SPM.1.SL.TZ0.8d.i:
Find .
-
17N.2.AHL.TZ0.H_11b.iii:
Hence show that can be expressed as .
-
17M.1.AHL.TZ2.H_9c:
By finding explain why is an increasing function.
-
18N.2.AHL.TZ0.H_9d:
Hence, or otherwise, solve the inequality .
-
16N.1.AHL.TZ0.H_11f:
Find the area of the region enclosed by the graph of and the -axis.
The curvature at any point on a graph is defined as .
-
21M.2.AHL.TZ1.11c:
Find the -coordinate of the point of inflexion.
-
17M.2.SL.TZ2.S_8c.ii:
Find the the rate of change of at B.
-
20N.2.SL.TZ0.S_10b:
Find the least value of .
-
20N.2.SL.TZ0.T_4a:
Write down an equation in and that shows this information.
-
18M.2.SL.TZ1.S_10b.ii:
For the graph of , write down the period.
-
19M.1.AHL.TZ2.H_8a:
Show that the volume of the cone may be expressed by .
-
17N.1.SL.TZ0.T_11b:
Write down the value of .
-
21M.3.AHL.TZ1.1c.i:
a point of inflexion with zero gradient.
-
21M.3.AHL.TZ1.1c.iii:
no points where the gradient is equal to zero.
-
21M.3.AHL.TZ1.1c.ii:
one local maximum point and one local minimum point.
-
21M.3.AHL.TZ1.1e.i:
exactly one -axis intercept.
-
20N.2.SL.TZ0.T_4f:
To prevent leaks, a sealant is applied to the interior surface of the bird bath.
Find the surface area to be covered by the sealant, given that the bird bath has maximum volume.
-
19N.2.SL.TZ0.S_8c.i:
Find the coordinates of .
-
SPM.1.SL.TZ0.9d:
The region R is enclosed by the graph of , the x-axis, and the vertical lines through the maximum point P and the point of inflexion Q.
Given that the area of R is 3, find the value of .
-
16N.1.AHL.TZ0.H_11e:
Sketch the graph of , clearly indicating the position of the local maximum point, the point of inflexion and the axes intercepts.
-
17N.2.AHL.TZ0.H_10c:
Find the coordinates of the point on the graph of where the normal to the graph is parallel to the line .
-
19M.2.SL.TZ2.S_5b:
Find the rate at which the population of fish is increasing at = 10.
-
SPM.1.SL.TZ0.9b:
Find the x-coordinate of P.
-
18N.1.AHL.TZ0.H_10d:
Find the area enclosed by the curve and the -axis between B and D, as shaded on the diagram.
-
18M.2.SL.TZ2.S_9c:
Write down the number of times that the acceleration of P is 0 m s−2 .
-
EXN.1.SL.TZ0.7b:
Find the dimensions of rectangle that has maximum perimeter and determine the value of the maximum perimeter.
-
18M.1.SL.TZ2.S_9a:
Express h in terms of r.
-
19N.1.SL.TZ0.S_8e:
Find the maximum volume.
-
19N.1.SL.TZ0.S_8d.ii:
Justify your answer.
-
19N.1.SL.TZ0.S_8c:
Find .
-
19M.1.SL.TZ2.T_15c:
Hence, find the number of vases that will maximize the profit.
-
EXN.1.SL.TZ0.7a:
Show that .
-
21M.3.AHL.TZ2.1f:
Hence, or otherwise, show that , for .
-
17N.1.SL.TZ0.S_6:
Let , for . The following diagram shows part of the graph of and the rectangle OABC, where A is on the negative -axis, B is on the graph of , and C is on the -axis.
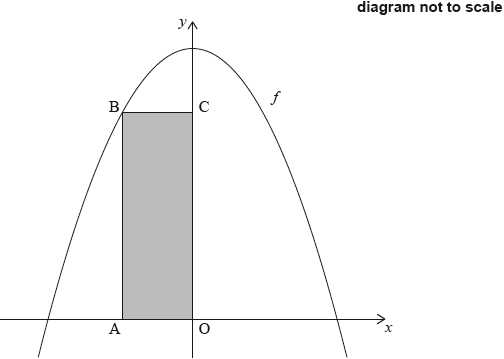
Find the -coordinate of A that gives the maximum area of OABC.
-
21M.3.AHL.TZ2.1g.ii:
a point of inflexion with zero gradient for odd values of , where and .
-
21M.3.AHL.TZ2.1h:
Consider the graph of , where , and .
State the conditions on and such that the equation has four solutions for .
-
SPM.1.SL.TZ0.9c:
Show that the x-coordinate of Q is .
-
21M.3.AHL.TZ1.1d.i:
the -coordinate of the local maximum point is .
-
SPM.1.SL.TZ0.8e:
The normal to the graph of at and the tangent to the graph of at intersect at the point (, ) .
Find the value of and the value of .
-
20N.2.SL.TZ0.S_10c:
Find .
-
19M.1.AHL.TZ2.H_8b:
Given that there is one inscribed cone having a maximum volume, show that the volume of this cone is .
-
EXN.1.SL.TZ0.7d:
Find the dimensions of rectangle that has maximum area.
-
17M.2.SL.TZ1.S_10a.i:
Write down the value of ;
-
21N.1.SL.TZ0.9a:
Find all the values of where the graph of is increasing. Justify your answer.
-
21N.1.SL.TZ0.9c.i:
Find the value of where the graph of has a local minimum. Justify your answer.
-
21N.1.SL.TZ0.9d:
The total area of the region enclosed by the graph of , the derivative of , and the -axis is .
Given that , find the value of .
-
22M.1.AHL.TZ2.11a:
Sketch the curve , clearly indicating any asymptotes with their equations. State the coordinates of any local maximum or minimum points and any points of intersection with the coordinate axes.
-
22M.3.AHL.TZ2.1b.i:
Write down the coordinates of the two points of inflexion on the curve .
-
22M.3.AHL.TZ2.1e:
Find the value of this -coordinate, giving your answer in the form , where .
-
21N.1.SL.TZ0.9b:
Find the value of where the graph of has a local maximum.
-
19M.1.SL.TZ1.T_15a:
Write down an equation for the area, , of the curved surface in terms of .
-
17N.1.SL.TZ0.T_11a:
Find the equation of the axis of symmetry of the graph of .
-
19M.1.SL.TZ2.T_15a:
Find the value of if no vases are sold.
-
17M.2.SL.TZ2.T_6d.i:
Write down the -coordinates of these two points;
-
17M.2.SL.TZ2.T_5c:
Find the value of that maximizes the area of the plot.
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
16N.2.SL.TZ0.T_6e:
Find .
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
18M.2.SL.TZ1.T_6a:
Write down the height of the cylinder.
-
18M.1.SL.TZ2.T_13b:
Find the value of s.
-
16N.1.AHL.TZ0.H_11g:
Find the value of the curvature of the graph of at the local maximum point.
-
18N.1.SL.TZ0.S_10b.ii:
Hence, find the equation of L in terms of .
-
18M.1.SL.TZ2.S_9c:
Given that there is a minimum value for C, find this minimum value in terms of .
-
17N.2.AHL.TZ0.H_11a.ii:
Sketch a graph of for .
-
18M.2.SL.TZ1.S_10c:
Hence, write in the form .
-
SPM.1.SL.TZ0.8d.ii:
Hence, use your answer to part (d)(i) to show that the graph of has a local minimum point at .
-
17N.1.SL.TZ0.T_15d:
Find the price, , that will give Maria the highest weekly profit.
-
EXN.1.AHL.TZ0.11e:
Show that the maximum value of is .
-
20N.2.SL.TZ0.T_4d:
Using your answer to part (c), find the value of for which is a maximum.
-
17N.2.AHL.TZ0.H_11c:
Solve the equation , giving your answers in the form where .
-
SPM.1.SL.TZ0.9a:
Show that .
-
17N.2.AHL.TZ0.H_10a.i:
Show that the -coordinate of the minimum point on the curve satisfies the equation .
-
17N.1.SL.TZ0.T_15b:
Find how much Maria earns in one week, from selling cheese, if the price of a kilogram of cheese is 8 EUR.
-
21M.3.AHL.TZ1.1e.iii:
exactly three -axis intercepts.
-
17N.2.AHL.TZ0.H_11a.iii:
Find the -coordinate(s) of the point(s) of inflexion of the graph of , labelling these clearly on the graph of .
-
17N.2.AHL.TZ0.H_10d:
This region is now rotated through radians about the -axis. Find the volume of revolution.
-
18N.1.AHL.TZ0.H_10c:
Find the -coordinates of A and of C , giving your answers in the form , where , .
-
17N.2.AHL.TZ0.H_11b.i:
Express in terms of .
-
16N.1.AHL.TZ0.H_11d:
Find the -coordinate of the point of inflexion of the graph of .
-
20N.2.SL.TZ0.S_10d:
Let be the region enclosed by the graph of , the -axis and the lines and . The area of is , correct to three significant figures.
Find .
-
18N.2.AHL.TZ0.H_9b:
Hence, or otherwise, find the coordinates of the point of inflexion on the graph of .
-
17N.2.AHL.TZ0.H_11b.ii:
Express in terms of .
-
EXN.2.AHL.TZ0.12d:
Use the differential equation to show that the points of zero gradient on the curve lie on two straight lines of the form where the values of are to be determined.
-
19M.2.SL.TZ1.S_4b:
Find the -coordinates of the points of inflexion of the graph of .
-
21M.2.AHL.TZ1.12e:
Find the value of when the rate of change of the population is at its maximum.
-
21M.3.AHL.TZ1.1d.ii:
the -coordinate of the local minimum point is .
-
21M.1.SL.TZ1.8c:
Given that , show that is a local maximum point.
-
21M.3.AHL.TZ1.1e.ii:
exactly two -axis intercepts.
-
21M.3.AHL.TZ2.1g.i:
a local minimum point for even values of , where and .
-
17M.2.SL.TZ1.S_10a.iii:
Write down the value of .
-
17M.2.SL.TZ1.S_10c:
Let be the vertical distance from a point on the graph of to the line . There is a point on the graph of where is a maximum.
Find the coordinates of P, where .
-
17M.2.SL.TZ1.S_10a.ii:
Write down the value of ;
-
17M.2.SL.TZ1.S_10b.ii:
Hence, find the area of the region enclosed by the graphs of and .
-
18N.2.SL.TZ0.T_6g:
Use your answer to part (f) to show that the width of Nanako’s bag is 12 cm.
-
17N.1.SL.TZ0.T_11c:
Find the value of and of .
-
19M.1.SL.TZ1.T_15c:
Find the value of when the area of the curved surface is maximized.
-
18N.2.SL.TZ0.T_6d:
Write down and simplify an expression in x and y for the area of cloth, A, used to make Nanako’s bag.
-
19M.1.SL.TZ2.T_15b:
Differentiate .
-
17N.1.SL.TZ0.T_15c:
Write down an expression for in terms of .
-
20N.2.SL.TZ0.T_4b:
Show that .
-
17M.2.SL.TZ2.T_6a:
Write down the -intercept of the graph.
-
17M.2.SL.TZ2.T_6c.i:
Show that .
-
17M.2.SL.TZ2.T_6b:
Find .
-
20N.2.SL.TZ0.T_4e:
Find the maximum volume of the bird bath.
-
17M.2.SL.TZ2.T_5b:
Write down the area of the plot in terms of .
-
19M.2.SL.TZ2.T_5h:
Determine the range of for ≤ ≤ .
-
17M.2.SL.TZ2.T_5a:
Show that the width of the plot, in metres, is given by .
-
17M.2.SL.TZ2.T_6g:
The equation , where , has four solutions. Find the possible values of .
-
20N.2.SL.TZ0.T_4c:
Find .
-
16N.2.SL.TZ0.T_6d:
Show that .
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
19M.1.SL.TZ1.T_15b:
Find .
-
18N.2.SL.TZ0.T_6e:
Use your answers to parts (c) and (d) to show that
.
-
18M.2.SL.TZ1.T_6d:
Show that the volume, V cm3 , of the new trash can is given by
.
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
18M.2.SL.TZ1.T_6f:
The designer claims that the new trash can has a capacity that is at least 40% greater than the capacity of the original trash can.
State whether the designer’s claim is correct. Justify your answer.
-
17M.2.SL.TZ2.T_5d:
Show that Violeta earns 5000 BGN from selling the flowers grown on the plot.
-
18M.2.SL.TZ1.T_4e:
Sketch the graph of y = f (x) for 0 < x ≤ 6 and −30 ≤ y ≤ 60.
Clearly indicate the minimum point P and the x-intercepts on your graph. -
17M.2.SL.TZ2.T_6c.ii:
Find .
-
17M.2.SL.TZ2.T_6d.ii:
Write down the intervals where the gradient of the graph of is positive.
-
17M.2.SL.TZ2.T_6e:
Write down the range of .
-
18N.2.SL.TZ0.T_6b:
Calculate the volume, in cm3, of the bag.
-
18N.2.SL.TZ0.T_6c:
Use this value to write down, and simplify, the equation in x and y for the volume of Nanako’s bag.
-
18N.2.SL.TZ0.T_6f:
Find .

