| Date | May 2014 | Marks available | 4 | Reference code | 14M.2.hl.TZ2.13 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | Express, Find, and Hence | Question number | 13 | Adapted from | N/A |
Question
The complex numbers \(u\) and \(v\) are represented by point A and point B respectively on an Argand diagram.
Point A is rotated through \(\frac{\pi }{2}\) in the anticlockwise direction about the origin O to become point \({\text{A}}'\). Point B is rotated through \(\frac{\pi }{2}\) in the clockwise direction about O to become point \({\text{B}}'\).
Consider \(z = r(\cos \theta + {\text{i}}\sin \theta ),{\text{ }}z \in \mathbb{C}\).
Use mathematical induction to prove that \({z^n} = {r^n}(\cos n\theta + {\text{i}}\sin n\theta ),{\text{ }}n \in {\mathbb{Z}^ + }\).
Given \(u = 1 + \sqrt 3 {\text{i}}\) and \(v = 1 - {\text{i}}\),
(i) express \(u\) and \(v\) in modulus-argument form;
(ii) hence find \({u^3}{v^4}\).
Plot point A and point B on the Argand diagram.
Find the area of triangle O\({\text{A}}'\)\({\text{B}}'\).
Given that \(u\) and \(v\) are roots of the equation \({z^4} + b{z^3} + c{z^2} + dz + e = 0\), where \(b,{\text{ }}c,{\text{ }}d,{\text{ }}e \in \mathbb{R}\),
find the values of \(b,{\text{ }}c,{\text{ }}d\) and \(e\).
Markscheme
let \({\text{P}}(n)\) be the proposition \({z^n} = {r^n}(\cos n\theta + {\rm{i}}\sin n\theta ),n \in {¢^ + }\)
let \(n = 1 \Rightarrow \)
\({\text{LHS}} = r(\cos \theta + {\text{i}}\sin \theta )\)
\({\text{RHS}} = r(\cos \theta + {\text{i}}\sin \theta ),{\text{ }}\therefore {\text{P}}(1)\) is true R1
assume true for \(n = k \Rightarrow {r^k}{(\cos \theta + {\text{i}}\sin \theta )^k} = {r^k}\left( {\cos (k\theta ) + {\text{i}}\sin (k\theta )} \right)\) M1
Note: Only award the M1 if truth is assumed.
now show \(n = k\) true implies \(n = k + 1\) also true
\({r^{k + 1}}{(\cos \theta + {\text{i}}\sin \theta )^{k + 1}} = {r^{k + 1}}{(\cos \theta + {\text{i}}\sin \theta )^k}(\cos \theta + {\text{i}}\sin \theta )\) M1
\( = {r^{k + 1}}\left( {\cos (k\theta ) + {\text{i}}\sin (k\theta )} \right)(\cos \theta + {\text{i}}\sin \theta )\)
\( = {r^{k + 1}}\left( {\cos (k\theta )\cos \theta - \sin (k\theta )\sin \theta + {\text{i}}\left( {\sin (k\theta )\cos \theta + \cos (k\theta )\sin \theta } \right)} \right)\) A1
\( = {r^{k + 1}}\left( {\cos (k\theta + \theta ) + {\text{i}}\sin (k\theta + \theta )} \right)\) A1
\( = {r^{k + 1}}\left( {\cos (k + 1)\theta + {\text{i}}\sin (k + 1)\theta } \right) \Rightarrow n = k + 1\) is true A1
\({\text{P}}(k)\) true implies \({\text{P}}(k + 1)\) true and \({\text{P}}(1)\) is true, therefore by mathematical induction statement is true for \(n \geqslant 1\) R1
Note: Only award the final R1 if the first 4 marks have been awarded.
[7 marks]
(i) \(u = 2{\text{cis}}\left( {\frac{\pi }{3}} \right)\) A1
\(v = \sqrt 2 {\text{cis}}\left( { - \frac{\pi }{4}} \right)\) A1
Notes: Accept 3 sf answers only. Accept equivalent forms.
Accept \(2{e^{\frac{\pi }{3}i}}\) and \(\sqrt 2 {e^{ - \frac{\pi }{4}i}}\).
(ii) \({u^3} = {2^3}{\text{cis}}(\pi ) = - 8\)
\({v^4} = 4{\text{cis}}( - \pi ) = - 4\) (M1)
\({u^3}{v^4} = 32\) A1
Notes: Award (M1) for an attempt to find \({u^3}\) and \({v^4}\).
Accept equivalent forms.
[4 marks]
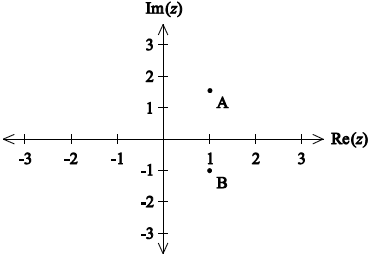 A1
A1
Note: Award A1 if A or \({\text{1 + }}\sqrt 3 i\) and B or \(1 - i\) are in their correct quadrants, are aligned vertically and it is clear that \(\left| u \right| > \left| v \right|\).
[1 mark]
Area \( = \frac{1}{2} \times 2 \times \sqrt 2 \times \sin \left( {\frac{{5\pi }}{{12}}} \right)\) M1A1
\( = 1.37{\text{ }}\left( { = \frac{{\sqrt 2 }}{4}\left( {\sqrt 6 + \sqrt 2 } \right)} \right)\) A1
Notes: Award M1A0A0 for using \(\frac{{7\pi }}{{12}}\).
[3 marks]
\((z - 1 + {\text{i}})(z - 1 - {\text{i}}) = {z^2} - 2z + 2\) M1A1
Note: Award M1 for recognition that a complex conjugate is also a root.
\(\left( {z - 1 - \sqrt 3 {\text{i}}} \right)\left( {z - 1 + \sqrt 3 {\text{i}}} \right) = {z^2} - 2z + 4\) A1
\(\left( {{z^2} - 2z + 2} \right)\left( {{z^2} - 2z + 4} \right) = {z^4} - 4{z^3} + 10{z^2} - 12z + 8\) M1A1
Note: Award M1 for an attempt to expand two quadratics.
[5 marks]

