| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.sl.TZ2.5 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Determine | Question number | 5 | Adapted from | N/A |
Question
Consider the propositions \(r\), \(p\) and \(q\).
Complete the following truth table.
Determine whether the compound proposition \(\neg \left( {(r \wedge p) \vee \neg q)} \right) \Leftrightarrow \neg (r \wedge p) \wedge q\) is a tautology, a contradiction or neither.
Give a reason.
Markscheme
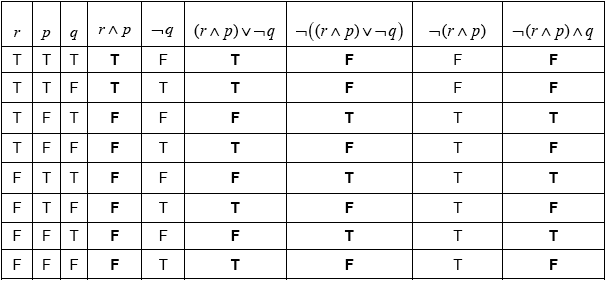(A1)(A1)(ft)(A1)(ft)(A1) (C4)
Notes: Award (A1) for each correct column.
For the “\({(r \wedge p) \vee \neg q}\)” follow through from the “\(r \wedge p\)” column.
For the “\(\neg \left( {(r \wedge p) \vee \neg q)} \right)\)” column, follow through from the preceding column.
tautology (A1)(ft)
columns \(\neg \left( {(r \wedge p) \vee \neg q)} \right)\) and \(\neg (r \wedge p) \wedge q\) are identical (R1)(C2)
Notes: Do not award (R0)(A1)(ft). Follow through from their table in part (a).
Award the (R1) for an additional column representing \(\neg \left( {(r \wedge p) \vee \neg q)} \right) \Leftrightarrow \neg (r \wedge p) \wedge q\) that is consistent with their table.
