| Date | May 2015 | Marks available | 2 | Reference code | 15M.2.sl.TZ1.2 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Copy and complete | Question number | 2 | Adapted from | N/A |
Question
Consider the following statements.
\(p\): the land has been purchased
\(q\): the building permit has been obtained
\(r\): the land can be used for residential purposes
Write the following argument in symbolic form.
“If the land has been purchased and the building permit has been obtained, then the land can be used for residential purposes.”
In your answer booklet, copy and complete a truth table for the argument in part (a).
Begin your truth table as follows.
Use your truth table to determine whether the argument in part (a) is valid.
Give a reason for your decision.
Write down the inverse of the argument in part (a)
(i) in symbolic form;
(ii) in words.
Markscheme
\((p \wedge q) \Rightarrow r\) (A1)(A1)(A1)
Notes: Award (A1) for conjunction seen, award (A1) for implication seen, award (A1) for correct simple propositions in correct order (the parentheses are required). Accept \(r \Leftarrow (p \wedge q)\).
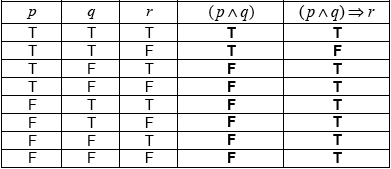 (A1)(ft)(A1)(ft)
(A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for each correct column, follow through to the final column from their \((p \wedge q)\) column. For the second (A1)(ft) to be awarded there must be an implication in part (a).
Follow through from part (a).
The argument is not valid since not all entries in the final column are T. (A1)(ft)(R1)
Notes: Do not award (A1)(ft)(R0). Follow through from part (b).
Accept “The argument is not valid since \((p \wedge q) \Rightarrow r\) is not a tautology”.
(i) \(\neg (p \wedge q) \Rightarrow \neg r\) (A1)(ft)(A1)(ft)
OR
\((\neg p \vee \neg q) \Rightarrow \neg r\) (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for the negation of their antecedent and the negation of their consequent, (A1)(ft) for their fully correct answer.
Follow through from part (a). Accept \(\neg r \Leftarrow \neg (p \wedge q)\) or \(\neg r \Leftarrow (\neg p \vee \neg q)\). Follow through from part (a).
(ii) if it is not the case that the land has been purchased and the building permit has been obtained then the land can not be used for residential purposes. (A1)(A1)(ft)
OR
if (either) the land has not been purchased or the building permit has not been obtained then the land can not be used for residential purposes. (A1)(A1)(ft)
Notes: Award (A1) for “if… then…” seen, (A1)(ft) for correct statements in correct order. Follow through from part (d)(i).
Examiners report
Forming the statement in part (a) was attainable by the great majority, although the lack of parentheses was a common fault.
The truth table in part (b) saw less success and it was clear that some centres simply had not prepared their candidates in this area of the course.
Where the truth table was correctly constructed many candidates were not aware of the conditions required for an argument to be valid and in part (d) the converse and the inverse were often confused.
Where the truth table was correctly constructed many candidates were not aware of the conditions required for an argument to be valid and in part (d) the converse and the inverse were often confused.

