| Date | May 2014 | Marks available | 3 | Reference code | 14M.1.sl.TZ2.10 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Calculate | Question number | 10 | Adapted from | N/A |
Question
Günter is at Berlin Tegel Airport watching the planes take off. He observes a plane that is at an angle of elevation of \(20^\circ\) from where he is standing at point \({\text{G}}\). The plane is at a height of 350 metres. This information is shown in the following diagram.
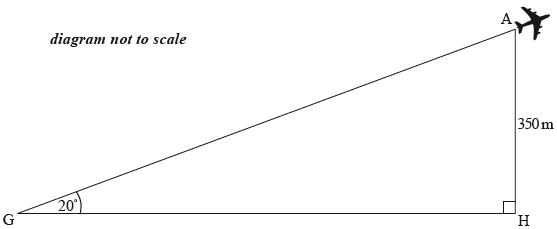
Calculate the horizontal distance, \({\text{GH}}\), of the plane from Günter. Give your answer to the nearest metre.
The plane took off from a point \({\text{T}}\), which is \(250\) metres from where Günter is standing, as shown in the following diagram.
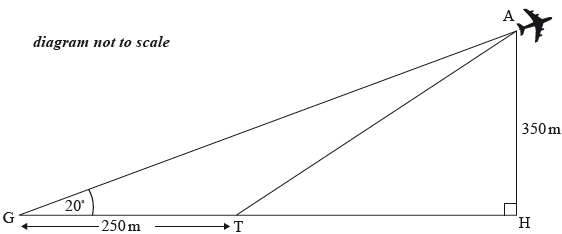
Using your answer from part (a), calculate the angle \({\text{ATH}}\), the takeoff angle of the plane.
Markscheme
\(\frac{{350}}{{\tan 20^\circ }}\) (M1)
\( = {\text{961.617}} \ldots \) (A1)
\( = 962{\text{ (m)}}\) (A1)(ft) (C3)
Notes: Award (M1) for correct substitution into correct formula, (A1) for correct answer, (A1)(ft) for correct rounding to the nearest metre.
Award (M0)(A0)(A0) for \(961\) without working.
[3 marks]
\({\text{961.617}} \ldots - 250 = {\text{711.617}} \ldots \) (A1)(ft)
\({\tan ^{ - 1}}\left( {\frac{{350}}{{{\text{711.617}} \ldots }}} \right)\) (M1)
\( = {\text{26.2}}^\circ {\text{ (26.1896}} \ldots {\text{)}}\) (A1)(ft) (C3)
Notes: Accept \(26.1774…\) from use of 3 sf answer \(962\) from part (a). Follow through from their answer to part (a).
Accept alternative methods.
[3 marks]

