| Date | November 2013 | Marks available | 2 | Reference code | 13N.1.sl.TZ0.5 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 5 | Adapted from | N/A |
Question
In triangle \({\text{ABC}}\), \({\text{AC}} = 20 {\text{ cm}}\), \({\text{BC}} = 12 {\text { cm}}\) and \({\rm{A\hat BC}} = 90^\circ\).
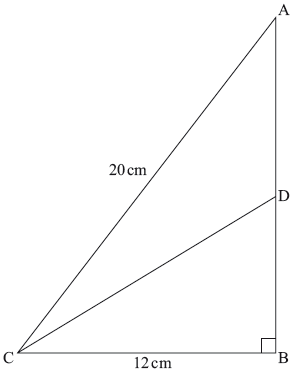 diagram not to scale
diagram not to scale
Find the length of \({\text{AB}}\).
\({\text{D}}\) is the point on \({\text{AB}}\) such that \(\tan ({\rm{D\hat CB}}) = 0.6\).
Find the length of \({\text{DB}}\).
\({\text{D}}\) is the point on \({\text{AB}}\) such that \(\tan ({\rm{D\hat CB}}) = 0.6\).
Find the area of triangle \({\text{ADC}}\).
Markscheme
\(({\text{A}}{{\text{B}}^2}) = {20^2} - {12^2}\) (M1)
Note: Award (M1) for correctly substituted Pythagoras formula.
\({\text{AB}} = 16{\text{ cm}}\) (A1) (C2)
[2 marks]
\(\frac{{{\text{DB}}}}{{12}} = 0.6\) (M1)
Note: Award (M1) for correct substitution in tangent ratio or equivalent ie seeing \(12 \times 0.6\).
\({\text{DB}} = 7.2{\text{ cm}}\) (A1) (C2)
Note: Award (M1)(A0) for using \(\tan 31\) to get an answer of \(7.21\).
Award (M1)(A0) for \(\frac{{12}}{{\sin 59}} = \frac{{{\text{DB}}}}{{\sin 31}}\) to get an answer of \(7.2103…\) or any other incorrect answer.
[2 marks]
\(\frac{1}{2} \times 12 \times (16 - 7.2)\) (M1)
Note: Award (M1) for their correct substitution in triangle area formula.
OR
\(\frac{1}{2} \times 12 \times 16 - \frac{1}{2} \times 12 \times 7.2\) (M1)
Note: Award (M1) for subtraction of their two correct area formulas.
\( = 52.8{\text{ c}}{{\text{m}}^2}\) (A1)(ft) (C2)
Notes: Follow through from parts (a) and (b).
Accept alternative methods.
[2 marks]
Examiners report
This question was not well answered. Many candidates could not use Pythagoras’ theorem correctly and many failed to appreciate the significance of \(\tan ( < {\text{DCB}}) = 0.6\) and calculated the size of the angle DCB, rounding it to 31°. Unfortunately, this method led to an inaccurate value for DB. Finding the area of triangle ADC was also difficult for many who did not realize that they needed to do a subtraction of triangle areas. Candidates who tried to find side lengths and angles for triangle ADC were generally unsuccessful in calculating its area.
This question was not well answered. Many candidates could not use Pythagoras’ theorem correctly and many failed to appreciate the significance of \(\tan ( < {\text{DCB}}) = 0.6\) and calculated the size of the angle DCB, rounding it to 31°. Unfortunately, this method led to an inaccurate value for DB. Finding the area of triangle ADC was also difficult for many who did not realize that they needed to do a subtraction of triangle areas. Candidates who tried to find side lengths and angles for triangle ADC were generally unsuccessful in calculating its area.
This question was not well answered. Many candidates could not use Pythagoras’ theorem correctly and many failed to appreciate the significance of \(\tan ( < {\text{DCB}}) = 0.6\) and calculated the size of the angle DCB, rounding it to 31°. Unfortunately, this method led to an inaccurate value for DB. Finding the area of triangle ADC was also difficult for many who did not realize that they needed to do a subtraction of triangle areas. Candidates who tried to find side lengths and angles for triangle ADC were generally unsuccessful in calculating its area.

