| Date | November 2016 | Marks available | 4 | Reference code | 16N.1.sl.TZ0.11 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Calculate | Question number | 11 | Adapted from | N/A |
Question
AC is a vertical communications tower with its base at C.
The tower has an observation deck, D, three quarters of the way to the top of the tower, A.
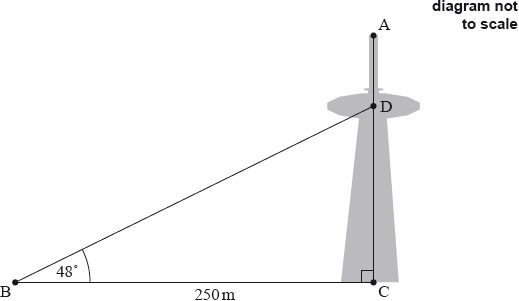
From a point B, on horizontal ground 250 m from C, the angle of elevation of D is 48°.
Calculate CD, the height of the observation deck above the ground.
Calculate the angle of depression from A to B.
Markscheme
\(\tan 48^\circ = \frac{{{\text{CD}}}}{{250}}\) (M1)
Note: Award (M1) for correct substitution into the tangent ratio.
\(({\text{CD}} = ){\text{ }}278{\text{ }}({\text{m}}){\text{ }}(277.653 \ldots )\) (A1) (C2)
[2 marks]
\(\tan {\text{ABC (or equivalent)}} = \frac{{\frac{4}{3} \times 277.653 \ldots }}{{250}}\) (M1)(M1)(M1)
Note: Award (M1) for \(\frac{4}{3}\) multiplying their part (a), (M1) for substitution into the tangent ratio, (M1) for correct substitution.
OR
\(90 - {\tan ^{ - 1}}\left( {\frac{{250}}{{\frac{4}{3} \times 277.653 \ldots }}} \right)\) (M1)(M1)(M1)
Note: Award (M1) for \(\frac{4}{3}\) multiplying their part (a), (M1) for substitution into the tangent ratio, (M1) for subtracting from 90 and for correct substitution.
\({\text{(angle of depression}} = {\text{) }}56.0^\circ {\text{ }}(55.9687 \ldots )\) (A1)(ft) (C4)
Note: Follow through from part (a).
[4 marks]

