| Date | May 2015 | Marks available | 2 | Reference code | 15M.2.sl.TZ1.4 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Calculate | Question number | 4 | Adapted from | N/A |
Question
A boat race takes place around a triangular course, \({\text{ABC}}\), with \({\text{AB}} = 700{\text{ m}}\), \({\text{BC}} = 900{\text{ m}}\) and angle \({\text{ABC}} = 110^\circ \). The race starts and finishes at point \({\text{A}}\).
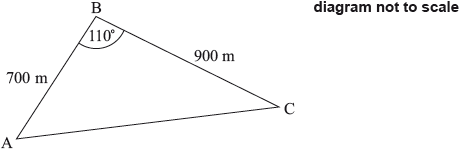
Calculate the total length of the course.
It is estimated that the fastest boat in the race can travel at an average speed of \(1.5\;{\text{m}}\,{{\text{s}}^{ - 1}}\).
Calculate an estimate of the winning time of the race. Give your answer to the nearest minute.
It is estimated that the fastest boat in the race can travel at an average speed of \(1.5\;{\text{m}}\,{{\text{s}}^{ - 1}}\).
Find the size of angle \({\text{ACB}}\).
To comply with safety regulations, the area inside the triangular course must be kept clear of other boats, and the shortest distance from \({\text{B}}\) to \({\text{AC}}\) must be greater than \(375\) metres.
Calculate the area that must be kept clear of boats.
To comply with safety regulations, the area inside the triangular course must be kept clear of other boats, and the shortest distance from \({\text{B}}\) to \({\text{AC}}\) must be greater than \(375\) metres.
Determine, giving a reason, whether the course complies with the safety regulations.
The race is filmed from a helicopter, \({\text{H}}\), which is flying vertically above point \({\text{A}}\).
The angle of elevation of \({\text{H}}\) from \({\text{B}}\) is \(15^\circ\).
Calculate the vertical height, \({\text{AH}}\), of the helicopter above \({\text{A}}\).
The race is filmed from a helicopter, \({\text{H}}\), which is flying vertically above point \({\text{A}}\).
The angle of elevation of \({\text{H}}\) from \({\text{B}}\) is \(15^\circ\).
Calculate the maximum possible distance from the helicopter to a boat on the course.
Markscheme
\({\text{A}}{{\text{C}}^2} = {700^2} + {900^2} - 2 \times 700 \times 900 \times \cos 110^\circ \) (M1)(A1)
\({\text{AC}} = 1315.65 \ldots \) (A1)(G2)
length of course \( = 2920{\text{ (m)}}\;\;\;(2915.65 \ldots {\text{ m)}}\) (A1)
Notes: Award (M1) for substitution into cosine rule formula, (A1) for correct substitution, (A1) for correct answer.
Award (G3) for \(2920\;\;\;(2915.65 \ldots )\) seen without working.
The final (A1) is awarded for adding \(900\) and \(700\) to their \({\text{AC}}\) irrespective of working seen.
\(\frac{{2915.65}}{{1.5}}\) (M1)
Note: Award (M1) for their length of course divided by \(1.5\).
Follow through from part (a).
\( = 1943.76 \ldots {\text{ (seconds)}}\) (A1)(ft)
\( = 32{\text{ (minutes)}}\) (A1)(ft)(G2)
Notes: Award the final (A1) for correct conversion of their answer in seconds to minutes, correct to the nearest minute.
Follow through from part (a).
\(\frac{{700}}{{\sin {\text{ACB}}}} = \frac{{1315.65 \ldots }}{{\sin 110^\circ }}\) (M1)(A1)(ft)
OR
\(\cos {\text{ACB}} = \frac{{{{900}^2} + 1315.65{ \ldots ^2} - {{700}^2}}}{{2 \times 900 \times 1315.65 \ldots }}\) (M1)(A1)(ft)
\({\text{ACB}} = 30.0^\circ \;\;\;(29.9979 \ldots ^\circ )\) (A1)(ft)(G2)
Notes: Award (M1) for substitution into sine rule or cosine rule formula, (A1) for their correct substitution, (A1) for correct answer.
Accept \(29.9^\circ\) for sine rule and \(29.8^\circ\) for cosine rule from use of correct three significant figure values. Follow through from their answer to (a).
\(\frac{1}{2} \times 700 \times 900 \times \sin 110^\circ \) (M1)(A1)
Note: Accept \(\frac{1}{2} \times {\text{their AC}} \times {\text{900}} \times {\text{sin(their ACB)}}\). Follow through from parts (a) and (c).
\( = 296000{\text{ }}{{\text{m}}^2}\;\;\;(296003{\text{ }}{{\text{m}}^2})\) (A1)(G2)
Notes: Award (M1) for substitution into area of triangle formula, (A1) for correct substitution, (A1) for correct answer.
Award (G1) if \(296000\) is seen without units or working.
\(\sin 29.9979 \ldots = \frac{{{\text{distance}}}}{{900}}\) (M1)
\({\text{(distance}} = ){\text{ }}450{\text{ (m)}}\;\;\;{\text{(449.971}} \ldots {\text{)}}\) (A1)(ft)(G2)
Note: Follow through from part (c).
OR
\(\frac{1}{2} \times {\text{distance}} \times 1315.65 \ldots = 296003\) (M1)
\(({\text{distance}} = ){\text{ }}450{\text{ (m)}}\;\;\;{\text{(449.971}} \ldots {\text{)}}\) (A1)(ft)(G2)
Note: Follow through from part (a) and part (d).
\(450\) is greater than \(375\), thus the course complies with the safety regulations (R1)
Notes: A comparison of their area from (d) and the area resulting from the use of \(375\) as the perpendicular distance is a valid approach and should be given full credit. Similarly a comparison of angle \({\text{ACB}}\) and \({\sin ^{ - 1}}\left( {\frac{{375}}{{900}}} \right)\) should be given full credit.
Award (R0) for correct answer without any working seen. Award (R1)(ft) for a justified reason consistent with their working.
Do not award (M0)(A0)(R1).
\(\tan 15^\circ = \frac{{{\text{AH}}}}{{700}}\) (M1)
Note: Award (M1) for correct substitution into trig formula.
\({\text{AH}} = 188{\text{ (m)}}\;\;\;(187.564 \ldots )\) (A1)(ft)(G2)
\({\text{H}}{{\text{C}}^2} = 187.564{ \ldots ^2} + 1315.65{ \ldots ^2}\) (M1)(A1)
Note: Award (M1) for substitution into Pythagoras, (A1) for their \(1315.65{ \ldots}\) and their \(187.564{ \ldots}\) correctly substituted in formula.
\({\text{HC}} = 1330 \ldots {\text{ (m)}}\;\;\;(1328.95 \ldots )\) (A1)(ft)(G2)
Note: Follow through from their answer to parts (a) and (f).
Examiners report
Most candidates were able to recognize and use the cosine rule correctly in part (a) and then to complete part (b) – though perhaps not giving the answer to the correct level of accuracy. It is expected that candidates can use “distance = speed x time” without the formula being given. The work involving sine rule was less successful, though correct responses were given by the great majority and the area of the course was again successfully completed by most candidates. A common error throughout these parts was the use of the total length of the course. A more fundamental error was the halving of the angle and/or the base in calculations – this error has been seen in a number of sessions and perhaps needs more emphasis.
Most candidates were able to recognize and use the cosine rule correctly in part (a) and then to complete part (b) – though perhaps not giving the answer to the correct level of accuracy. It is expected that candidates can use “distance = speed x time” without the formula being given. The work involving sine rule was less successful, though correct responses were given by the great majority and the area of the course was again successfully completed by most candidates. A common error throughout these parts was the use of the total length of the course. A more fundamental error was the halving of the angle and/or the base in calculations – this error has been seen in a number of sessions and perhaps needs more emphasis.
Most candidates were able to recognize and use the cosine rule correctly in part (a) and then to complete part (b) – though perhaps not giving the answer to the correct level of accuracy. It is expected that candidates can use “distance = speed x time” without the formula being given. The work involving sine rule was less successful, though correct responses were given by the great majority and the area of the course was again successfully completed by most candidates. A common error throughout these parts was the use of the total length of the course. A more fundamental error was the halving of the angle and/or the base in calculations – this error has been seen in a number of sessions and perhaps needs more emphasis.
Most candidates were able to recognize and use the cosine rule correctly in part (a) and then to complete part (b) – though perhaps not giving the answer to the correct level of accuracy. It is expected that candidates can use “distance = speed x time” without the formula being given. The work involving sine rule was less successful, though correct responses were given by the great majority and the area of the course was again successfully completed by most candidates. A common error throughout these parts was the use of the total length of the course. A more fundamental error was the halving of the angle and/or the base in calculations – this error has been seen in a number of sessions and perhaps needs more emphasis.
In part (e), unless evidence was presented, reasoning marks did not accrue; the interpretative nature of this part was a significant discriminator in determining the quality of a response.
There were many instances of parts (f) and (g) being left blank and angle of elevation is still not well understood. Again, the interpretative nature of part (g) – even when part (f) was correct – caused difficulties
There were many instances of parts (f) and (g) being left blank and angle of elevation is still not well understood. Again, the interpretative nature of part (g) – even when part (f) was correct – caused difficulties

