| Date | May 2011 | Marks available | 2 | Reference code | 11M.2.sl.TZ2.2 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find and Hence | Question number | 2 | Adapted from | N/A |
Question
Let \(g(x) = \frac{1}{2}x\sin x\) , for \(0 \le x \le 4\) .
Sketch the graph of g on the following set of axes.
Hence find the value of x for which \(g(x) = - 1\) .
Markscheme
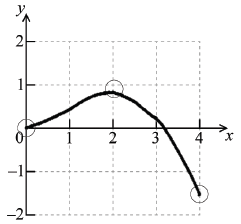 A1A1A1A1 N4
A1A1A1A1 N4
Note: Award A1 for approximately correct shape, A1 for left end point in circle, A1 for local maximum in circle, A1 for right end point in circle.
[4 marks]
attempting to solve \(g(x) = - 1\) (M1)
e.g. marking coordinate on graph, \(\frac{1}{2}x\sin x + 1 = 0\)
\(x = 3.71\) A1 N2
[2 marks]
Examiners report
This question was well done by the majority of candidates. Most sketched an approximately correct shape in the given domain, though some candidates did not realize they had to set their GDC to radians, producing a meaningless sketch. Candidates need to be aware that unless otherwise specified, questions will expect radians to be used. The most confident candidates used a table to aid their graphing. Although most recognized the need of the GDC to answer part (b), some used the trace function, hence obtaining an inaccurate result, while others attempted a fruitless analytical approach. Merely stating "using GDC" is insufficient evidence of method; a sketch or an equation set equal to zero are both examples of appropriate evidence.
This question was well done by the majority of candidates. Most sketched an approximately correct shape in the given domain, though some candidates did not realize they had to set their GDC to radians, producing a meaningless sketch. Candidates need to be aware that unless otherwise specified, questions will expect radians to be used. The most confident candidates used a table to aid their graphing. Although most recognized the need of the GDC to answer part (b), some used the trace function, hence obtaining an inaccurate result, while others attempted a fruitless analytical approach. Merely stating "using GDC" is insufficient evidence of method; a sketch or an equation set equal to zero are both examples of appropriate evidence.

