| Date | May 2010 | Marks available | 2 | Reference code | 10M.2.sl.TZ2.5 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Write down | Question number | 5 | Adapted from | N/A |
Question
Consider \(f(x) = 2 - {x^2}\) , for \( - 2 \le x \le 2\) and \(g(x) = \sin {{\rm{e}}^x}\) , for \( - 2 \le x \le 2\) . The graph of f is given below.
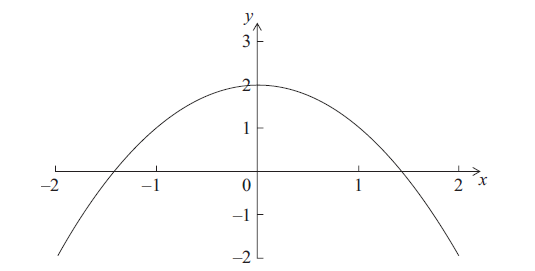
On the diagram above, sketch the graph of g.
Solve \(f(x) = g(x)\) .
Write down the set of values of x such that \(f(x) > g(x)\) .
Markscheme
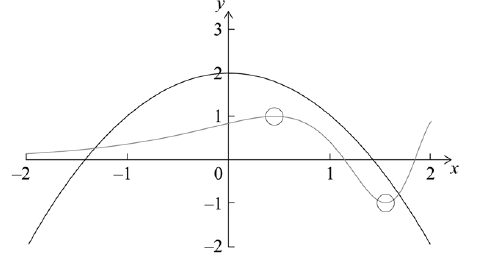A1A1A1 N3
[3 marks]
\(x = - 1.32\) , \(x = 1.68\) (accept \(x = - 1.41\) , \(x = 1.39\) if working in degrees) A1A1 N2
[2 marks]
\( - 1.32 < x < 1.68\) (accept \( - 1.41 < x < 1.39\) if working in degrees) A2 N2
[2 marks]
Examiners report
This question was answered well by a pleasing number of candidates.
For part (a), many good graphs were seen, though a significant number of candidates either used degrees or a function such as \(\sin {{\rm{e}}^x}\) . There were students who lost marks for poor diagrams. For example, the shape was correct but the maximum and minimum were not accurate enough.
There were candidates who struggled in vain to solve the equation in part (b) algebraically instead of using a GDC. Those that did use their GDCs to solve the equation frequently gave their answers inaccurately, suggesting that they did not know how to use the "zero" function on their calculator but found a rough solution using the "trace" function.
In part (c) they often gave the correct solution, or obtained follow-through marks on their incorrect results to part (b).
