| Date | May 2015 | Marks available | 3 | Reference code | 15M.1.sl.TZ1.8 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find and Write down | Question number | 8 | Adapted from | N/A |
Question
A line \(L\) passes through points \({\text{A}}( - 2,{\text{ }}4,{\text{ }}3)\) and \({\text{B}}( - 1,{\text{ }}3,{\text{ }}1)\).
(i) Show that \(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 1 \\ { - 1} \\ { - 2} \end{array}} \right)\).
(ii) Find \(\left| {\overrightarrow {{\text{AB}}} } \right|\).
Find a vector equation for \(L\).
The following diagram shows the line \(L\) and the origin \(O\). The point \(C\) also lies on \(L\).
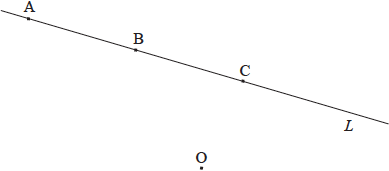
Point \(C\) has position vector \(\left( {\begin{array}{*{20}{c}} 0 \\ y \\ { - 1} \end{array}} \right)\).
Show that \(y = 2\).
(i) Find \(\overrightarrow {{\text{OC}}} \bullet \overrightarrow {{\text{AB}}} \).
(ii) Hence, write down the size of the angle between \(C\) and \(L\).
Hence or otherwise, find the area of triangle \(OAB\).
Markscheme
(i) correct approach A1
eg\(\;\;\;{\text{B}} - {\text{A, AO}} + {\text{OB}}\)
\(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 1 \\ { - 1} \\ { - 2} \end{array}} \right)\) AG N0
(ii) correct substitution (A1)
eg\(\;\;\;\sqrt {{{(1)}^2} + {{( - 1)}^2} + {{( - 2)}^2}} ,{\text{ }}\sqrt {1 + 1 + 4} \)
\(\left| {\overrightarrow {{\text{AB}}} } \right| = \sqrt 6 \) A1 N2
[3 marks]
any correct equation in the form \(r = a + tb\) (any parameter for \(t\))
where \(a\) is \(\left( {\begin{array}{*{20}{c}} { - 2} \\ 4 \\ 3 \end{array}} \right)\) or \(\left( {\begin{array}{*{20}{c}} { - 1} \\ 3 \\ 1 \end{array}} \right)\) and \(b\) is a scalar multiple of \(\left( {\begin{array}{*{20}{c}} 1 \\ { - 1} \\ { - 2} \end{array}} \right)\) A2 N2
eg\(\;\;\;\(r\) = \left( {\begin{array}{*{20}{c}} { - 2} \\ 4 \\ 3 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 1 \\ { - 1} \\ { - 2} \end{array}} \right),{\text{ }}(x,{\text{ }}y,{\text{ }}z) = ( - 1,{\text{ }}3,{\text{ }}1) + t(1,{\text{ }} - 1,{\text{ }} - 2),{\text{ }}{\mathbf{r}} = \left( {\begin{array}{*{20}{c}} { - 1 + t} \\ {3 - t} \\ {1 - 2t} \end{array}} \right)\)
Note: Award A1 for the form \({\mathbf{a}} + t{\mathbf{b}}\), A1 for the form \(L = {\mathbf{a}} + t{\mathbf{b}}\), A0 for the form \({\mathbf{r}} = {\mathbf{b}} + t{\mathbf{a}}\).
METHOD 1
valid approach (M1)
eg\(\;\;\;\left( {\begin{array}{*{20}{c}} { - 1} \\ 3 \\ 1 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 1 \\ { - 1} \\ { - 2} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 \\ y \\ { - 1} \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} 0 \\ y \\ { - 1} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - 2} \\ 4 \\ 3 \end{array}} \right) + s\left( {\begin{array}{*{20}{c}} 1 \\ { - 1} \\ { - 2} \end{array}} \right)\)
one correct equation from their approach A1
eg\(\;\;\; - 1 + t = 0,{\text{ }}1 - 2t = - 1,{\text{ }} - 2 + s = 0,{\text{ }}3 - 2s = - 1\)
one correct value for their parameter and equation A1
eg\(\;\;\;t = 1,{\text{ }}s = 2\)
correct substitution A1
eg\(\;\;\;3 + 1( - 1),{\text{ }}4 + 2( - 1)\)
\(y = 2\) AG N0
METHOD 2
valid approach (M1)
eg\(\;\;\;\overrightarrow {{\text{AC}}} = k\overrightarrow {{\text{AB}}} \)
correct working A1
eg\(\;\;\;\overrightarrow {{\text{AC}}} = \left( {\begin{array}{*{20}{c}} 2 \\ {y - 4} \\ { - 4} \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} 2 \\ {y - 4} \\ { - 4} \end{array}} \right) = k\left( {\begin{array}{*{20}{c}} 1 \\ { - 1} \\ { - 2} \end{array}} \right)\)
\(k = 2\) A1
correct substitution A1
eg\(\;\;\;y - 4 = - 2\)
\(y = 2\) AG N0
[4 marks]
(i) correct substitution A1
eg\(\;\;\;0(1) + 2( - 1) - 1( - 2),{\text{ }}0 - 2 + 2\)
\(\overrightarrow {{\text{OC}}} \bullet \overrightarrow {{\text{AB}}} = 0\) A1 N1
(ii) \(9{0^ \circ }\) or \(\frac{\pi }{2}\) A1 N1
[3 marks]
METHOD 1 \({\text{(area}} = 0.5 \times {\text{height}} \times {\text{base)}}\)
\(\left| {\overrightarrow {{\text{OC}}} } \right| = \sqrt {0 + {2^2} + {{( - 1)}^2}} \;\;\;\left( { = \sqrt 5 } \right)\;\;\;\)(seen anywhere) A1
valid approach (M1)
eg\(\;\;\;\frac{1}{2} \times \left| {\overrightarrow {{\text{AB}}} } \right| \times \left| {\overrightarrow {{\text{OC}}} } \right|,{\text{ }}\left| {\overrightarrow {{\text{OC}}} } \right|\) is height of triangle
correct substitution A1
eg\(\;\;\;\frac{1}{2} \times \sqrt 6 \times \sqrt {0 + {{(2)}^2} + {{( - 1)}^2}} ,{\text{ }}\frac{1}{2} \times \sqrt 6 \times \sqrt 5 \)
area is \(\frac{{\sqrt {30} }}{2}\) A1 N2
METHOD 2 (difference of two areas)
one correct magnitude (seen anywhere) A1
eg\(\;\;\;\left| {\overrightarrow {{\text{OC}}} } \right| = \sqrt {{2^2} + {{( - 1)}^2}} \;\;\;\left( { = \sqrt 5 } \right),\;\;\;\left| {\overrightarrow {{\text{AC}}} } \right| = \sqrt {4 + 4 + 16} \;\;\;\left( { = \sqrt {24} } \right),\;\;\;\left| {\overrightarrow {{\text{BC}}} } \right| = \sqrt 6 \)
valid approach (M1)
eg\(\;\;\;\Delta {\text{OAC}} - \Delta {\text{OBC}}\)
correct substitution A1
eg\(\;\;\;\frac{1}{2} \times \sqrt {24} \times \sqrt 5 - \frac{1}{2} \times \sqrt 5 \times \sqrt 6 \)
area is \(\frac{{\sqrt {30} }}{2}\) A1 N2
METHOD 3 \({\text{(area}} = \frac{1}{2}ab\sin C{\text{ for }}\Delta {\text{OAB)}}\)
one correct magnitude of \(\overrightarrow {{\text{OA}}} \) or \(\overrightarrow {{\text{OB}}} \) (seen anywhere) A1
eg\(\;\;\;\left| {\overrightarrow {{\text{OA}}} } \right| = \sqrt {{{( - 2)}^2} + {4^2} + {3^2}} \;\;\;\left( { = \sqrt {29} } \right),\;\;\;\left| {\overrightarrow {{\text{OB}}} } \right| = \sqrt {1 + 9 + 1} \;\;\;\left( { = \sqrt {11} } \right)\)
valid attempt to find \(\cos \theta \) or \(\sin \theta \) (M1)
eg\(\;\;\;\cos {\text{C}} = \frac{{ - 1 - 3 - 2}}{{\sqrt 6 \times \sqrt {11} }}\;\;\;\left( { = \frac{{ - 6}}{{\sqrt {66} }}} \right),\;\;\;29 = 6 + 11 - 2\sqrt 6 \sqrt {11} \cos \theta ,{\text{ }}\frac{{\sin \theta }}{{\sqrt 5 }} = \frac{{\sin 90}}{{\sqrt {29} }}\)
correct substitution into \(\frac{1}{2}ab\sin {\text{C}}\) A1
eg\(\;\;\;\frac{1}{2} \times \sqrt 6 \times \sqrt {11} \times \sqrt {1 - \frac{{36}}{{66}}} ,{\text{ }}0.5 \times \sqrt 6 \times \sqrt {29} \times \frac{{\sqrt 5 }}{{\sqrt {29} }}\)
area is \(\frac{{\sqrt {30} }}{2}\) A1 N2
[4 marks]
Total [16 marks]
Examiners report
Finding \(\overrightarrow {{\text{AB}}} \) and its magnitude were mostly well done.
Mostly correct answers with common errors being using both position vectors or writing it as “\(L = \)” instead of “\({\mathbf{r}} = \)”.
Many candidates assumed that \(\overrightarrow {{\text{AB}}} = \overrightarrow {{\text{BC}}} \), although this was not indicated on the diagram nor given in the question.
Mostly this was well answered. A surprising number of candidates wrote the scalar product as a vector \((0,{\text{ }} - 2,{\text{ }}2)\). In part b) many missed the clue given by the phrase “hence, write down” and carried out a calculation for cosine theta using the scalar product again.
This part was poorly done. Few candidates realised how to directly calculate the area based on their previous work and could not see the “height” of the obtuse triangle as \(\left| {\overrightarrow {{\text{OC}}} } \right|\). Those who tried to use \(A = \frac{1}{2}ab\sin C\) had trouble generating the angle. Those who subtracted areas \((\Delta {\text{OAC}} - \Delta {\text{OBC)}}\) were usually successful.

