| Date | May 2014 | Marks available | 4 | Reference code | 14M.2.sl.TZ1.4 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
The following diagram shows two perpendicular vectors u and v.
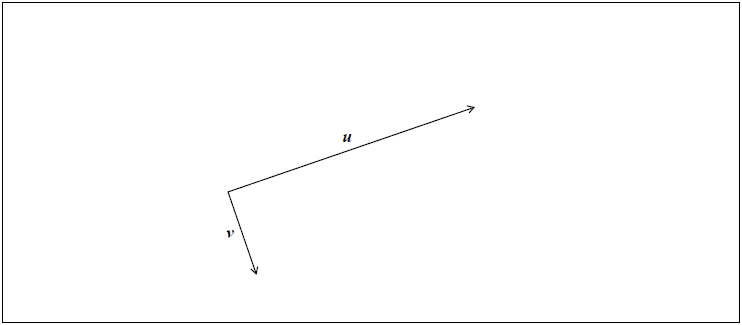
Let \(w = u - v\). Represent \(w\) on the diagram above.
Given that \(u = \left( \begin{array}{c}3\\2\\1\end{array} \right)\) and \(v = \left( \begin{array}{c}5\\n\\3\end{array} \right)\), where \(n \in \mathbb{Z}\), find \(n\).
Markscheme
METHOD 1
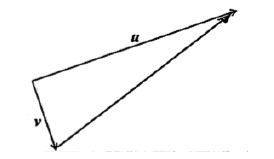 A1A1 N2
A1A1 N2
Note: Award A1 for segment connecting endpoints and A1 for direction (must see arrow).
METHOD 2
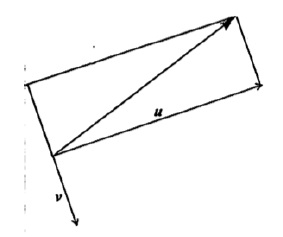 A1A1 N2
A1A1 N2
Notes: Award A1 for segment connecting endpoints and A1 for direction (must see arrow).
Additional lines not required.
[2 marks]
evidence of setting scalar product equal to zero (seen anywhere) R1
eg u \( \cdot \) v \( = 0,{\text{ }}15 + 2n + 3 = 0\)
correct expression for scalar product (A1)
eg \(3 \times 5 + 2 \times n + 1 \times 3,{\text{ }}2n + 18 = 0\)
attempt to solve equation (M1)
eg \(2n = - 18\)
\(n = - 9\) A1 N3
[4 marks]

