 In an electrical circuit, electrons move due to potential difference. Electric fields caused by charged plates, point charges or charged spheres cause lone charges to accelerate. This changes their energy.
In an electrical circuit, electrons move due to potential difference. Electric fields caused by charged plates, point charges or charged spheres cause lone charges to accelerate. This changes their energy.
Key Concepts
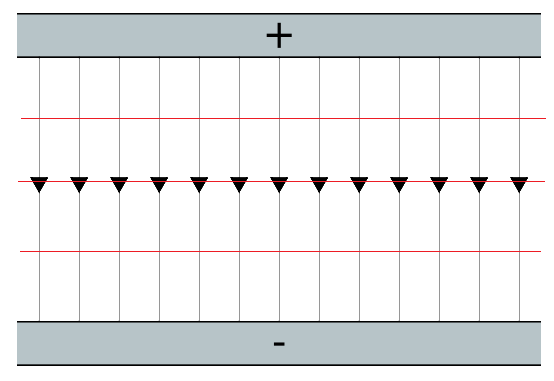
A uniform field has a constant field strength. Field lines are equidistant and parallel, and show the direction of force acting on a positive test charge. Uniform electric fields are formed between oppositely charged parallel plates.

Beyond the edges of the plates, the field would no longer be uniform, but these are not drawn.
Electric field strength is defined as the force per unit charge:
\(E={F_e\over q}\)
Field strength is equal to the magnitude of the potential gradient:
\(E={V_e\over d}\)
These equations are often combined, for example to find the force acting on a given charge:
\({F_e\over q}={V_e\over d}\)
- \(E\) is electric field strength (NC-1 or Vm-1)
- \(F_e\) is electric force (N)
- \(q\) is the charge placed in the field (C)
- \(V_e\) is the potential difference between the plates (V)
- \(d\) is the distance between the plates (m)
The energy changes that take place in electric fields are between electric potential energy and kinetic energy:
- Work can be done by a charge on the field if it moves towards the plate of like charge; the charge loses kinetic energy and gains potential energy.
- Work is done by the field on the charge if it is attracted to the plate of opposite charge; the charge loses potential energy and gains kinetic energy.
Since electric field strength is constant, the force acting on the charge is constant everywhere. Work is done when a charge moves along a field line, perpendicular to the plates:
\(W=F_{e}s=\Delta E_p=q\Delta V_e\)
- \(W\) is work done (J)
- \(F_e\) is electric force (N)
- \(s\) is displacement parallel to field lines (m)
- \(\Delta E_p\) is change in potential energy (J)
- \(q\) is charge (C)
- \(\Delta V_e\) is potential difference
No work is done parallel to the plates. This is because the charge would be moving along an equipotential surface.
Radial fields are produced by point charges or charged spheres. Field strength increases with proximity to the charge. This is indicated by closer field lines. The direction of the field lines shows the direction of force acting on a positive test charge placed in the field.

As radial fields are non-unifom, electric force and field strength are not constant. Electric force is found using Coulomb's law:
\(F_e=k{Qq\over r^2}\)
Electric field strength is the force per unit charge:
\(E={F_e\over q}=k{Q\over r^2}\)
- \(E\) is electric field strength (NC-1)
- \(F_e\) is electric force (N)
- \(q\) is the charge placed in the field (C)
- \(k\) is a constant (8.99×109 N m2 C−2)
- \(Q\) is the charge producing the field (C)
- \(r\) is the distance between the centres of the charges (m)
Electric potential is the work done per unit charge in bringing a positive test charge from infinity to a point in an electric field at a small constant speed.
As force is not constant, electric potential is found by integrating the force with respect to distance from infinity:
\(V_e={\int_\infty^r F_e\,\mathrm{d}r\over q}= {\int_\infty^r {kQq\over r^2}\,\mathrm{d}r\over q}\)
\(\Rightarrow V_e=k{Q\over r}\)
- \(V_e\) is electric potential (JC-1 or V)
- \(k\) is a constant (8.99×109 N m2 C−2)
- \(Q\) is the charge producing the field (C)
- \(r\) is the distance between the centres of the charges (m)
As with energy and work done, potential is a scalar quantity.
Energy is changed when an object is moved through a distance by a force. When a charge is moved into or out of a non-uniform electric field, it will be attracted or repelled. Therefore, work is done and energy becomes stored in the charge itself. This energy is electrical potential energy and is measured in J.
\(E_p=qV_e=k{Qq\over r}\)
The equipotential surfaces in a radial field are spherical, shown as circles on a 2-dimensional diagram. As potential varies with \(1\over r\) from the centre of the charge, the equipotentials increase in spacing outward from the centre.
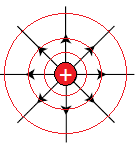
Work is done when a charge is moved between equipotentials:
\(W=q\Delta V_e=q\times kQ({1\over r_f}-{1\over r_i})\)
- \(W\) is work done (J)
- \(q\) is the moving charge (C)
- \(\Delta V_e\) is electric potential difference (JC-1 or V)
- \(k\) is a constant (8.99×109 N m2 C−2)
- \(Q\) is the charge producing the field (C)
- \(r\) is the initial or final distance between the centres of the charges (m)
Potential gradient is the ratio of the difference in potential to the distance between the equipotential surfaces. Its magnitude is equal to electric field strength:
\(E=-{\Delta V_e\over \Delta r}\)
- \(E\) is electric field strength (NC-1)
- \(\Delta V_e\) is potential difference (JC-1 or V)
- \(\Delta r\) is the distance between the potentials (m)
So far we have examined only the electric field outside of the charge producing the field. What about the field strengths and potentials at radii less than the radius of the sphere?
- A sphere may have uniform distribution of charge:
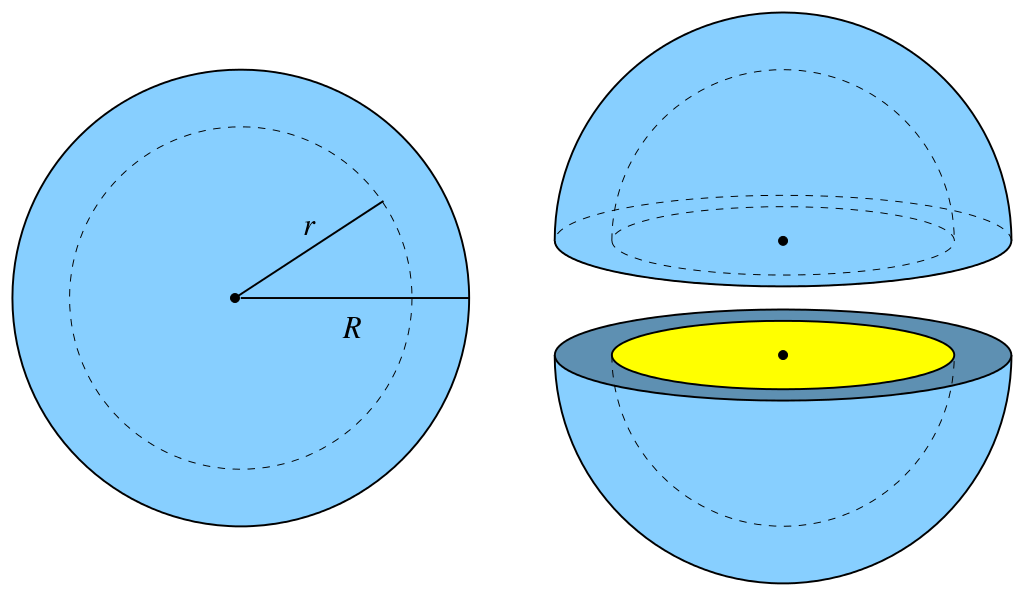
By Ag2gaeh - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=49540033
The charge enclosed within the sphere by a radius \(r\) in comparison with the total radius \(R\) is related to the volume:
\({q\over Q}={r^3\over R^3}\)
\(E=k{q\over r^2}=k{Qr\over R^3}\)
\(V_e=k{q\over r}=k{Qr^2\over R^3}\)
- The sphere may alternatively be a conductor. In this case the charge would move to the surface. In this situation, the field at any radius within the sphere would be zero; the potential would be the same as at the surface.
Use flashcards to practise your recall.
Use quizzes to practise application of theory.
START QUIZ!
Electric potential 1/1
A small test charge is close to a sphere of charge.
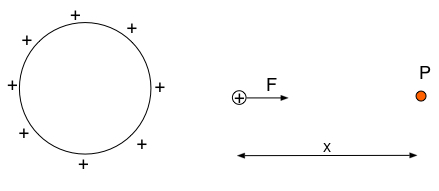
If point P is at zero potential the potential energy the electrical PE of the test charge is not equal to
The force is not constant so work done will not equal Fx
Which of the following lines gives the correct relationship between electric potential of a point charge and distance from it.
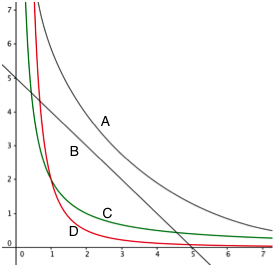
V is proportional to 1/r
A small test charge q is moved from infinity to a point close to a sphere of charge Q and the force measured
The potential can be found from:
Work done for a small step = Fx
Potential = work done/q
The graph below shows the line of y = 1/x

The area of the shaded part is:
Area of a trapezium = 1/2(y1 +y2)Δx
The small test charge moves from right to left between the two charges shown.
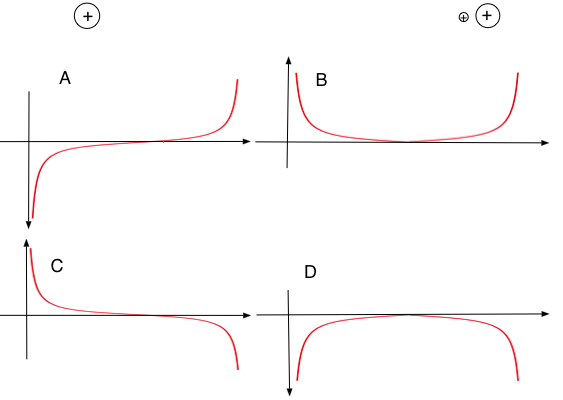
Which graph represents the force experienced by the test charge vs distance from the left hand charge?
Force is to the left (-) when furthest to the right and to the right (+) when close to the charge on the left
The diagram represents a 2C test charge so far from a sphere of charge that there is no force experienced by it.

The amount of work done moving to P is 10 J. The potential at P is
Potential is work done per unit charge
The graph represents the force applied to a 2C test charge as it is moved in an electric field.

The change in potential is
Work done = area = 1/2 x 8 x 4 = 16 J
Potential = work done/charge
The diagram represents the path of a 2 C test charge moving between A and B via a path that passes through points C and D. The potential at these points is shown.
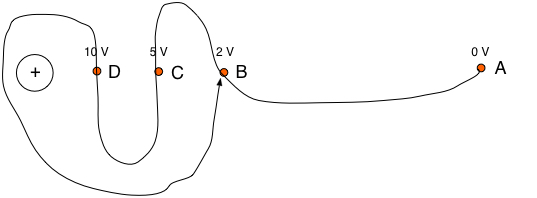
The work done is
The work done is independent of path- Work done = potential difference x charge
The diagram represents a charge with two lines of equipotential, one at 10 V the other at 20 V.

The work done moving the 2 C test charge from A to B is
The potential at B is the same as A as it is on the same line of equipotential
The diagram represents a charge with two lines of equipotential, one at 10 V the other at 20 V.

The work done moving the 2 C test charge from A to C is
The potential difference = 10 V
Work done = Vq
The potential at the surface of a charged sphere, so far from the Earth that the force on it is negligible, is 10 V. The potential at the surface of the Earth is 100 V.
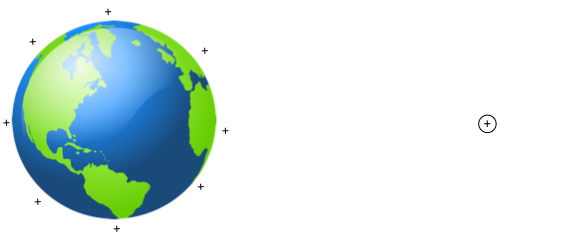
If the sphere is moved close to the surface of the Earth the potential at its surface will be
Potential will be higher due to presence of the Earth.
Two spheres so far from the Earth that the electric force is negligible, have potentials shown.

Both charges are moved close to the Earth. The potential difference between the charges will be
The charges will have potential 110 V and 112 V so pd is 2 V.
The diagram represents 2 charged spheres close to the Earth-
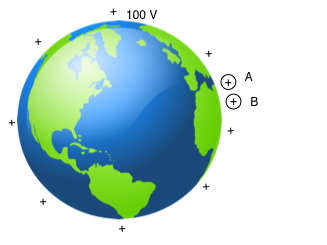
The potential at the Earth´s surface is 100 V and the potential difference between A and B is 2 V.
What is the potential difference between A and B when the potential of the Earth is raised to 200 V?
The potential of both charges will be raised by 100 V.
How much of AHL Electric fields have you understood?
Feedback
Which of the following best describes your feedback?
Notes
Report a problem for flashcard
Your best time:


 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn