 There are many questions you can expect to answer after studying Magnetism! Why is the North pole actually a South? Why do we define magnetic field in terms of rotation not acceleration? What is the connection between magnetic fields and electric current? And why don't magnetic waves exist without electric waves?
There are many questions you can expect to answer after studying Magnetism! Why is the North pole actually a South? Why do we define magnetic field in terms of rotation not acceleration? What is the connection between magnetic fields and electric current? And why don't magnetic waves exist without electric waves?
Key Concepts
Iron is the most common magnetic material. This means that it contains magnetic domains that can be aligned to make the material into a magnet. Iron is an essential component in the alloy steel. Nichol and cobalt are also magnetic.
 There are several ways of categorising magnets:
There are several ways of categorising magnets:
- Permanent magnets (produced by aligning the magnetic domains in a material, made from hard magnetic materials like steel) - usually purchased as bar magnets
- Temporary magnets (also produced by aligning magnetic domains, made from soft magnetic materials like iron)
- Electromagnets (produced by moving charges, made from any electrical conductor) - usually the wire is wrapped into a coil, known as a solenoid
NB: How could you test if an object is a magnet?
Permanent magnets
Electromagnets
Force on a current-carrying conductor
A current-carrying conductor (i.e. an electromagnet) within an existing magnetic field will experience a force due to the interactions of the magnetic fields. This is often known as the motor effect.
If the field is perpendicular to the current the the force is perpendicular to both.
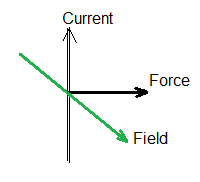

- Splay the thumb and first two fingers of your left hand to create three right angles. Practise rotating this arrangement at the wrist, elbow and shoulder without disrupting the right angles.
- Your first finger represents the external magnetic field. Line this orientation up first towards south.
- Keeping the field direction, rotate your left hand until your second finger lines up with the conventional current.
- Your thumb will now be pointing in a direction that is perpendicular to both of the previous directions. Your thumb is pointing in the direction that the current-carrying conductor will move.


Calculating forces - conductors

- flux density (B) in T
- current (I) in A
- length of conductor in the field (L) in m
\(F=BIL\)
This force is used to define the ampere: 1 A is the current that would cause a force of 2 x 10-7 Nm-1 between two long parallel conductors placed in a vacuum.

Calculating forces - individual charges

- flux density (B) in T
- charge (q) in C
- velocity at which the charge is moving (v) in ms-1
\(F=Bqv\)


How much of Magnetic fields have you understood?


 The term flux comes from a time when magnetic field was thought to be caused by the flow of a substance through space.
The term flux comes from a time when magnetic field was thought to be caused by the flow of a substance through space. Bar magnets and solenoids have two poles: north and south. A theoretical isolated north pole is attracted to a south pole and repelled by a north pole. Similar to charges: unlike poles attract, like poles repel
Bar magnets and solenoids have two poles: north and south. A theoretical isolated north pole is attracted to a south pole and repelled by a north pole. Similar to charges: unlike poles attract, like poles repel



 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn