 Max, Min and Optimisation
Max, Min and Optimisation
This is the part where we learn about how we use calculus to solve different kinds of problems. So far we have spent a lot of time learning about how calculus helps us to work out the gradient of given function for any given point. In this section we focus on the points where the gradient is zero. These are called the local maxima and minima and crucial in what we call 'optimisation' where we try to work out how to maximise profits or minimise costs and so on.
In this unit you should learn to…
-
Find where the gradient of a function is zero
-
Find local maximum and minimum points
-
Use calculus to solve an optimisation problem
This video is about finding the value of x when the function has a gradient of zero and how we use calculus to do this.
In this video we extend the idea to functions that have more than one point where the gradient is zero and how to distinguish between them.
This video is about finding local maxima and minima and distinguishing between them using the second derivative.
In this video we get a first look at how an optimisation problem that we need calculus to solve.
Often an optimisation problem requires you to put some information together to first make a model. This video offers some examples and help with that idea.
This is an extension of the above idea, but looks at some of the more complicated examples.
Now we put these ideas together all in one problem. This video covers making the model.
Revision Cards - Review this condensed 'key point' revision card to help you check and keep ideas fresh in your mind.

Self Checking Quiz
Practice your understanding on these questions. Check your answers when you are done and read the hints where you got stuck. If you find there are still some gaps in your understanding then go back to the videos and slides above. Depending on how confident you are with these ideas, this might take 2-3 hours to complete and you should work with a pen and paper to hand.
Question 1
Consider the function \(f(x)={ x }^{ 2 }-4x+7\)
then \(f'(x)\quad =\quad ax\quad +\quad b\)
a) What are the values of a and b?
b) What is the value of x when the gradient is zero.
c) And so if the coordinates of the vertex are (x,y), what are the values of x and y?
a) a = , b =
b) x =
c) x = , y =
a) Function differentiates to \(f'(x)\quad =\quad 2x-4\) (careful, since it is -4, but the equation says +b, then b must be negative.
b) \(when\quad gradient\quad =\quad 0,\\ f'(x)\quad =\quad 2x-4\quad =\quad 0\\ so,\quad 2x\quad =\quad 4\\ and\quad x\quad =\quad 2\)
c) \(At\quad vertex,\quad f'(x)\quad =\quad 0\quad so\quad x\quad =\quad 2\\ Substitute\quad x\quad =\quad 2\quad into\quad f(x)={ x }^{ 2 }-4x+7\\ So,\quad y\quad =\quad 3\) (You might use your table function here)
Question 2
Consider the function \(f(x)={ x }^{ 2 }+6x+3\)
then \(f'(x)\quad =\quad ax\quad +\quad b\)
a) What are the values of a and b?
b) What is the value of x when the gradient is zero.
c) And so if the coordinates of the vertex are (x,y), what are the values of x and y?
a) a = , b =
b) x =
c) x = , y =
a) Function differentiates to \(f'(x)\quad =\quad 2x+6\)
b) \(when\quad gradient\quad =\quad 0,\\ f'(x)\quad =\quad 2x+6\quad =\quad 0\\ so,\quad 2x\quad =\quad -6\\ and\quad x\quad =\quad -3\)
c) \(At\quad vertex,\quad f'(x)\quad =\quad 0\quad so\quad x\quad =\quad -3\\ Substitute\quad x\quad =\quad -3\quad into\quad f(x)={ x }^{ 2 }+6x+3\\ So,\quad y\quad =\quad -6\) (You might use your table function here)
Question 3
Consider the function \(f(x)=\frac { 1 }{ 3 } { x }^{ 3 }-\frac { 1 }{ 2 } { x }^{ 2 }-12x+4\)
Then \(f'(x)=a{ x }^{ 2 }+b{ x }+c\)
a) What are the values of a, b and c?
b) What are the values of x when the gradient is zero? (Give your answers in numerical order)
c) What are the coordinates of the local maximum and minimum for this function
a) a = , b = , c =
b) x = , x =
c) Local maximum x = , y = (give y to 3sf)
Local Minimum, x = , y = (give y to 3sf)
a) \(f'(x)={ x }^{ 2 }-{ x }-12\)(Pay attention to the negative signs)
b) \(When\quad the\quad gradient\quad is\quad zero\\ f'(x)={ x }^{ 2 }-{ x }-12\quad =\quad 0\\ f'(x)=(x+3)(x-4)\quad =\quad 0\\ x\quad =\quad -3\quad or\quad 4\) You can use the polynomial solver on your GDC to solve this equation
c) Read the gradient function from your GDC for x = -3 and x = 4
Question 4
Consider the function \(f(x)={ 2x }^{ 2 }+\frac { 32 }{ x } \)
a) This can be written as, \(f(x)={ 2x }^{ 2 }+m{ x }^{ n }\), what are the values of m and n
b) The derivative of the function is given by \(f'(x)\quad =\quad ax+b{ x }^{ c }\)what are the values of a, b and c?
c) At what value of x is the gradient = 0?
d) What are the coordiantes of this local minimum?
a) m = , n =
b) a = , b = , c =
c) x =
d) x = , y =
a) BEWARE you are NOT differentiating here, you are just expressing it as a negative index. Remember...
\(\frac { 1 }{ { x }^{ n } } ={ x }^{ -n }\quad and\quad \frac { 3 }{ { x }^{ n } } ={ 3x }^{ -n }\quad and\quad \frac { 2 }{ { 5x }^{ n } } =\frac { 2 }{ 5 } { x }^{ -n }\) so \(f(x)={ 2x }^{ 2 }+\frac { 32 }{ x } \quad =\quad f(x)={ 2x }^{ 2 }+32{ x }^{ -1 }\)
...
b) \(if,\quad f(x)={ 2x }^{ 2 }+32{ x }^{ -1 },\quad then,\quad f'(x)\quad =\quad 4x-32{ x }^{ -2 }\)
...
c) \(when\quad gradient\quad =\quad 0,\\ f'(x)\quad =\quad 4x-32{ x }^{ -2 }\quad =\quad 0\\ f'(x)\quad =\quad 4x-\frac { 32 }{ { x }^{ 2 } } =0\\ so\quad 4x\quad =\quad \frac { 32 }{ { x }^{ 2 } } \\ and,\quad 4{ x }^{ 3 }\quad =\quad 32\\ and\quad { x }^{ 3 }\quad =\quad 8,\quad \\ so\quad x\quad =\quad 2\) Again, your equation solver on the GDC can do this for you.
...
d) \(At\quad vertex,\quad f'(x)\quad =\quad 0\quad so\quad x\quad =\quad 2\\ Substitute\quad x\quad =\quad 2\quad into\quad f(x)={ 2x }^{ 2 }+\frac { 32 }{ x } \\ So,\quad y\quad =\quad 24\) Again, the table function will help you to avoid mistakes
Question 5
The Volume of water (V) in a container varies with some given conditions against time (t), The Volume, \(V{ cm }^{ 3 }\) , is given by \(V=400+3t-{ t }^{ 2 }\)
a) If \(\frac { dV }{ dt } =at+b\) then what are the values of a and b?
b) At what value of t will the volume be at a maximum?
c) What will the maximum volume be?
a) a = , b =
b) t = (give the exact answer as a decimal)
c) Maximum Volume =
a) \(if\quad V=400+3t-{ t }^{ 2 }\quad then,\frac { dV }{ dt } =3-2t\)
b) \(at\quad maximum,\quad \frac { dV }{ dt } =3-2t=0\\ so,\quad 3=2t\\ and\quad t=\frac { 3 }{ 2 } =1.5\)
c) \(Maximum\quad occurs\quad at\quad t\quad =\quad 1.5\\ when\quad t=1.5\\ V=400+3(1.5)-{ (1.5) }^{ 2 }\\ V=400+4.5-2.25\\ V=402.25,\quad V=402{ cm }^{ 3 }\quad (3sf)\)
Using the GDC, if you enter the Volume function and have the derivative switched on then you can see that at t = 1.5, Volume is 402.25 and the derivative is zero.

Question 6
A company's profit, P, in 1000s of euros can be modelled by the the function, \(P(x)=19x-0.07{ x }^{ 2 }-10\)where \(x\), is a measure of units of product for the company.
a) if \(\frac { dP}{ dx } =ax+b,\)what are the values of a and b?
b) At what value of x while the profit be at a maximum?
c) Use the rounded answer to part b) to calculate the value of the maximum profit.
a) a = , b =
b) x = (give your answer to 3sf)
c) Maximum profit, P = (give your answer as the number of 1000s to 3sf)
a) \(if\quad P(x)=19x-0.07{ x }^{ 2 }-10,\quad then,\frac { dP }{ dx } =19-0.14x\)
b) \(At\quad maximum,\quad \frac { dP }{ dx } =19-0.14x=0\\ 19=0.14x\\ x=\frac { 19 }{ 0.14 } =135.71428.....\\ x=\quad 136\quad (3sf)\)
c) \(maximum\quad profit\quad occurs\quad at\quad x\quad =\quad 136\\ Substituting\quad in\quad to\quad P(x)=19x-0.07{ x }^{ 2 }-10\\ gives\quad V=1279.2\\ V=1280\quad (3sf)\)
Question 7
Consider the formula A = bh which is subject to the constraint that b - h=10.
a) Which of the expressions is the correct expression for A in terms of b?
b) If \(\frac { dA }{ db } =mb+n\), what are the values of m and n?
c) For what value of b is A a minimum?
d) What is the minimum value of A?
b) m = , n =
c) b =
d) Minimum value of A =
a) \(A=bh\\ b-h=10\quad so\\ b=10+h\quad and\\ b-10=h\\ Substitute\quad h\quad =\quad b-10\\ A=b(b-10)\\ A={ b }^{ 2 }-10b\)
b) \(if\quad A={ b }^{ 2 }-10b\\ then\quad \frac { dA }{ db } =2b-10\)
c) \(at\quad minimum\quad value,\quad \frac { dA }{ db } =2b-10=0\\ so\quad 2b=10\\ and\quad b=5\)
d) \(Substitute\quad b=5\quad into\quad A={ b }^{ 2 }-10b\\ so\quad A=-25\)
Question 8
Consider the formula \(A={ x }^{ 3 }+2xh\), subject to the condition that \(h=\frac { 3 }{ { x }^{ 3 } } \)
a) A can be expressed in terms of x only like this, \(A={ x }^{ 3 }+p{ x }^{ q }\), what are the values of p and q?
b) \(\frac { dA }{ dx } =m{ x }^{ 2 }-n{ x }^{ -3 }\), what are the values of m and n?
c) For what value of x is A at a local minimum?
a) p = , q =
b) m = , n =
c) x = (Answer to 3sf)
a) Substitute the value for h in to the expression for A,
\(if\quad A={ x }^{ 3 }+2xh\quad and\quad h=\frac { 3 }{ { x }^{ 3 } } \\ Substituting\quad gives\\ A={ x }^{ 3 }+\frac { 2x\times 3 }{ { x }^{ 3 } } \\ A={ x }^{ 3 }+\frac { 6x }{ { x }^{ 3 } } \\ A={ x }^{ 3 }+\frac { 6 }{ { x }^{ 2 } } \\ A={ x }^{ 3 }+6{ x }^{ -2 }\)
b) Differentiate A with respect to x
\(if\quad A={ x }^{ 3 }+6{ x }^{ -2 }\\ \\ then,\frac { dA }{ dx } =3{ x }^{ 2 }-12{ x }^{ -3 }\)
c) Solve for gradient = 0
\(At\quad minimum,\quad \frac { dA }{ dx } =3{ x }^{ 2 }-12{ x }^{ -3 }=0\\ 3{ x }^{ 2 }-12{ x }^{ -3 }=0\quad (use\quad GDC\quad solver)\\ x=1.3195....\\ x=1.32\quad (3sf)\)
Question 9
A closed cuboid box has Volume, \(V={ x }^{ 2 }h\). Its surface area, A, is limted to \(600{ cm }^{ 2 }\)
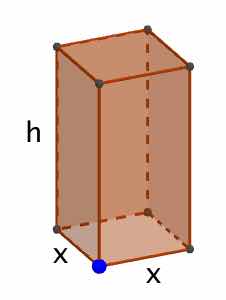 Dimensions shown are in cm
Dimensions shown are in cm
a) A is given by \(A=m{ x }^{ 2 }+nxh\), what are the values of m and n?
b) Since A = 600, we can say that \(\frac { a-{ x }^{ 2 } }{ bx } =h\), what are the values of a and b?
c) Use this expression for h to express the volume in terms of h only, where \(V=px-\frac { 1 }{ 2 } { x }^{ q }\), what are the values of p and q?
d) For what value of x is the Volume at a maximum?
e) What is the maximum volume?
f) What will the value of h be at this volume?
a) m = , n =
b) a = , b =
c) p = , q =
d) x = cm
e) Maximum Volume = \({ cm }^{ 3 }\)
f) h = cm
a) \(Area\quad is\quad the\quad 6\quad faces\quad added\quad together\\ A\quad =\quad 2{ x }^{ 2 }+2xh+2xh\\ A=2{ x }^{ 2 }+4xh\)
b) This part is tricky but is all about making h the subject of the formula
\(A=2{ x }^{ 2 }+4xh\\ 600=2{ x }^{ 2 }+4xh\\ 600-2{ x }^{ 2 }=4xh\\ \frac { 600-2{ x }^{ 2 } }{ 4x } =h\\ \frac { 300-{ x }^{ 2 } }{ 2x } =h\)
c) This stage involves substitutuing the expression for h in to the expression for volume.
\(Since\quad V{ =x }^{ 2 }h\quad and\quad h=\frac { 300-{ x }^{ 2 } }{ 2x } \\ V=\frac { { x }^{ 2 }(300-{ x }^{ 2 }) }{ 2x } \\ V=\frac { 300{ x }^{ 2 }-{ x }^{ 4 } }{ 2x } \\ (Divide\quad through\quad by\quad 2x)\\ V=150x-\frac { 1 }{ 2 } { x }^{ 3 }\)
d) Differentiate the function and solve for gradient = 0
\(if\quad V=150x-\frac { 1 }{ 2 } { x }^{ 3 }\quad then,\frac { dV }{ dx } =150-\frac { 3 }{ 2 } { x }^{ 2 }\\ Volume\quad is\quad a\quad maximum\quad when\quad \frac { dV }{ dx } =150-\frac { 3 }{ 2 } { x }^{ 2 }=0\\ 150=\frac { 3 }{ 2 } { x }^{ 2 }\\ 300=3{ x }^{ 2 }\\ 100={ x }^{ 2 }\\ x=\quad 10\quad (-10\quad is\quad not\quad in\quad the\quad valid\quad range)\)
e) This involves substituting the value of x that gives a minimum into the expression for volume.
\(Maximum\quad occurs\quad at\quad x=\quad 10\\ substitute\quad x=10\quad into\quad V=150x-\frac { 1 }{ 2 } { x }^{ 3 }\\ V=1000{ cm }^{ 3 }\)
f) Now substitute the value of x in to the expression for h.
\(Since\quad \frac { 300-{ x }^{ 2 } }{ 2x } =h\quad and\quad x=10\\ then,\quad \frac { 300-100 }{ 20 } =h\\ 10=h\)
Question 10
Consider a closed cylinder, radius r, height, h, whose volume must be 400\({ cm }^{ 3 }\). The aim is to minimise the Surface area, A, required to make the cylinder.
a) if the height h, can be expressed as \(h=\frac { a }{ \pi { r }^{ b } } \), what are the values of a and b?
b) The surface area of the cylinder can be expressed as \(A=2\pi { r }^{ 2 }+p{ r }^{ q }\), what are the values of p and q?
c) What value of r will give the minimum surface area?
d) Use the rounded answer to the part c) to work out,
i) The value of h when A is a minimum
ii) The minimum value of A
a) a = , b =
b) p = , q =
c) r = (Answer correct to 3sf)
d) i) h = cm , ii) A = cm2 (answers to 3sf)
a) Use the formula for volume of a cylinder and rearrange.
\(V=\pi { r }^{ 2 }h\quad and\quad is\quad given\quad as\quad 400{ cm }^{ 3 }\\ then\\ 400=\pi { r }^{ 2 }h\\ and\quad so,\quad h=\frac { 400 }{ \pi { r }^{ 2 } } \)
b) Use the formula for surface area of a cylinder and substitute the expression for h, then simplify.
\(A=2\pi { r }^{ 2 }+2\pi { r }h\quad and\quad h=\frac { 400 }{ \pi { r }^{ 2 } } \\ Substituting\quad for\quad h,\\ A=2\pi { r }^{ 2 }+\frac { 2\pi { r }\times 400 }{ \pi { r }^{ 2 } } \\ Cancelling\quad common\quad factors\\ A=2\pi { r }^{ 2 }+\frac { 800 }{ { r } } \\ A=2\pi { r }^{ 2 }+800{ r }^{ -1 }\)
c) Solve for gradient = 0. Perfectly acceptable to use the solve function to do this.
\(If\quad A=2\pi { r }^{ 2 }+800{ r }^{ -1 },\quad then\quad \frac { dA }{ dr } =4\pi { r }-800{ r }^{ -2 }\\ At\quad minimum,\quad \frac { dA }{ dr } =4\pi { r }-800{ r }^{ -2 }=0\\ 4\pi { r }=800{ r }^{ -2 }\\ 4\pi { r }=\frac { 800 }{ { r }^{ 2 } } \\ 4\pi { r }^{ 3 }=800\\ { r }^{ 3 }=\frac { 800 }{ 4\pi } \\ r=\sqrt [ 3 ]{ \frac { 800 }{ 4\pi } } \\ r=3.9929454...\\ r=3.99\quad cm\quad (3sf)\)
d) Substitutions can be done using the table function on your GDC or otherwise.
i) \(Substitute\quad r=3.99\quad in\quad to\quad h=\frac { 400 }{ \pi { r }^{ 2 } } \\ h=7.997685...\\ h=8.00cm\quad (3sf)\)
ii) \(Substitute\quad r=3.99\quad in\quad to\quad A=2\pi { r }^{ 2 }+800{ r }^{ -1 }\\ A=300.5301915...\\ A=\quad 301{ cm }^{ 2 }\quad (3sf)\)
The following questions are based on IB exam style questions from past exams. You should print these off (from the document at the top) and try to do these questions under exam conditions. Then you can check your work with the video solution.
How much of 5.6 & 5.7 Stationary Points and Optimisation have you understood?
Feedback
Which of the following best describes your feedback?




















 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn