 This page deals with all the counting principles in the HL course: Arrangements, Permutations and Combinations. You need to be familiar with combinations for the Binomial Theorem, but it is also useful in its own right to be able to work out, for example, how many ways there are of getting a hand of blackjack in a card game or finding how many different tickets are possible in a lottery. There is always more than one way of solving a problem. This page will enable to be confident in several methods, in order that you can have a flexible problem-solving strategy.
This page deals with all the counting principles in the HL course: Arrangements, Permutations and Combinations. You need to be familiar with combinations for the Binomial Theorem, but it is also useful in its own right to be able to work out, for example, how many ways there are of getting a hand of blackjack in a card game or finding how many different tickets are possible in a lottery. There is always more than one way of solving a problem. This page will enable to be confident in several methods, in order that you can have a flexible problem-solving strategy.
Try this quiz to practise questions about arrangements
START QUIZ!
Arrangements 1/1

4 different coloured bowls are arranged in a line. How many different arrangements are there?
Arrangements =
The objects are different, so there are 4! different arrangements
4! = 4 x 3 x 2 x 1 = 24

5 cards are arranged in a line. How many different possible arrangements are there?
Arrangements =
The objects are different, so there are 5! different arrangements
5! = 5 x 4 x 3 x 2 x 1 = 120

The 6 cards are placed in a line. How many different arrangements are there?
*Note that the cards with a coin are identical
Arrangements =
There are 6 objects and 3 of them are repeated.
There are \(\frac{6!}{3!}\)arrangements
\(\frac{6!}{3!}=\frac{6\cdot5\cdot4\cdot3\cdot 2\cdot1}{3\cdot2\cdot 1}=6\cdot5\cdot4=120\)

The coloured blocks are arranged in a line.
How many different arrangements are there?
Arrangements =
There are 6 objects. The trapezia are repeated 2 times. The rhombus ar repeated 2 times.
There are \(\frac{6!}{2!\cdot2!}=180\) arrangements
The letters from the word MATHEMATICS are placed in a line.
How many different arrangements are there?
The are 11 objects. The M , A ,T are repeated 2 times each.
There are \(\frac{11!}{2!\cdot2!\cdot2!}\) arrangements

The coloured rods are placed in a line. How many different arrangements are there?
There are 7 objects.The purple rods are repeated 3 times. The green rods are repeated 2 times.
There are \(\frac{7!}{3!\cdot2!}\) arrangements

8 different coloured rods are placed in a line.
How many different arrangements are there so that the blue and the green rods are together?
Think about the blue and green rods as one object.
This means that there now are 7 objects.
These 7 objects can be arranged in 7! ways.
For each of these arrangements, it is possible to reverse the order of the blue and green rods
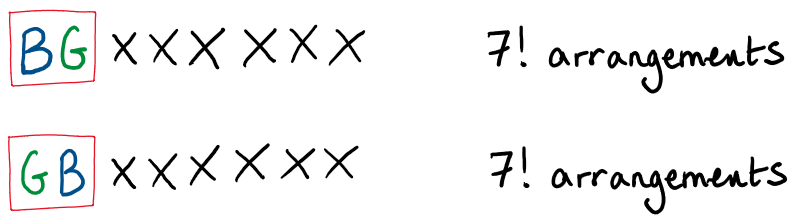
There are 2x7! different arrangements

10 cards are placed in a line. How many different ways can they be arranged so that the cards 1, 2 & 3 are together?
Think of the cards 1, 2 & 3 as one object.
This makes 8 objects with 8! arrangements.
There are 3! ways of arranging the numbers 1, 2 & 3
For each of these arrangements, it is possible to rearrange the items 1 , 2 & 3
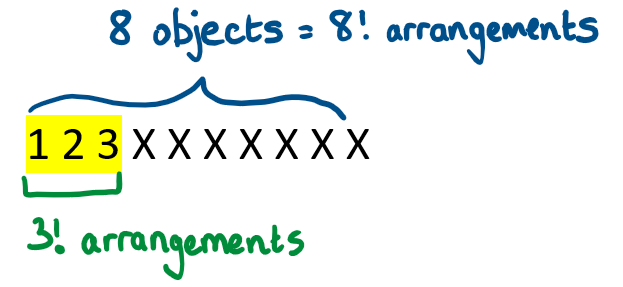
There are 3!x8!

6 different coloured bowls are placed in a line. How many arrangements are there in which the pink and red bowls are separated?
Arrangements =
The pink and red bowls are either separated or together.
Find the number of arrangements in total = 6!
Find the number of arrangements in which the pink and red bowls are together = 2x5!
The number of arrangements in which the pink and red bowls are separated = 6 - 2x5! = 480
Three men and two women stand together in a line.
In how many arrangements will all the men stand next to each and all the women stand next to each other?
Arrangements =
Think of the men as 1 object. Think of the women as 1 object.
There are 2 ways of arranging these 2 objects
There are 3! arrangements of men. There are 2! arrangements of women.
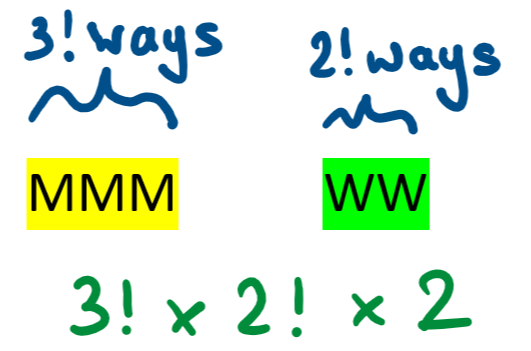
There are 3! x 2! x 2 = 24 arrangements
Try this quiz to practise questions about combinations and permutations
START QUIZ!
Combinations and Permutations 1/1

In a card game, two images are chosen from the card.
How many different possible ways are there if order is not important?
Number of ways =
Since order is not important, then this is a combination. We chose 2 items from 8 objects
\(^{8}C_2=\frac{8!}{6!2!}=\frac{8\cdot7}{2}=28\)
\(^{n}C_2=36\)
Work out n
n =
\(^{n}C_2=\frac{n!}{(n-2)!2!}=\frac{n(n-1)}{2}\)
We need to solve \(\frac{n(n-1)}{2}=36\)
n(n - 1) = 72
We can solve this quadratic equation, but it is clear that n = 9
Since 9x8 = 72

These 10 cards are shuffled thoroughly and 3 are dealt.
What is the probability of getting 3 cards containing 1 , 2 & 3
Since order is not important, then this is a combination. We chose 3 items from 10 objects
\(^{10}C_3=\frac{10!}{7!3!}=120\)
There is only one correct combination, so the probability is \(\frac{1}{120}\)
Alternatively, we can think of the probability of getting three consecutive correct cards.
There is a \(\frac{3}{10}\) chance that the first card is correct
There is a \(\frac{2}{9}\) chance that the second card is correct
There is a \(\frac{1}{8}\) chance that the third card is correct
The probability = \(\frac{3}{10}\cdot\frac{2}{9}\cdot\frac{1}{8}=\frac{1}{120}\)

These 5 cards are shuffled thoroughly and 2 cards are dealt.
What is the probability that the 1 card is dealt followed by the 2 card.
Since order is important this is a permutation question.
We chose 2 items from 5 objects
\(^{5}P_2=\frac{5!}{3!}=20\)
There is only one correct permutation, so the probability is \(\frac{1}{20}\)
Alternatively, we can think of the probability of getting two consecutive correct cards.
There is a \(\frac{1}{5}\) chance that the first card is correct
There is a \(\frac{2}{4}\) chance that the second card is correct
The probability = \(\frac{1}{5}\cdot\frac{1}{4}=\frac{1}{20}\)

Four letters are selected at random from these letters.
What is the probability that the letters can be put together to spell ZERO?
Since order is not important, then this is a combination. We chose 4 items from 8 objects
\(^{8}C_4=\frac{8!}{4!4!}=70\)
There is only one correct combination, so the probability is \(\frac{1}{70}\)
Alternatively, we can think of the probability of getting four consecutive correct letters.
The probability = \(\frac{4}{8}\cdot\frac{3}{7}\cdot\frac{2}{6}\cdot\frac{1}{5}=\frac{1}{70}\)
In the game of Blackjack, you are dealt 2 cards from a pack of 52 cards. To get a score of 21, you need an ace and a card of value 10 (10, J, Q or K).
How many different ways are there of getting a score of 21?

Number of ways =
Since order is not important, then this is a combination.
We need an ace: we chose 1 item from 4 objects
We need an 10 value card: we chose 1 item from 16 objects
There are 4x16 ways of getting 21

Four letters are chosen at random from RANDOMLY.
The probability that all letters chosen are consonants = \(\frac{a}{70}\)
Work out the value of a
*For the purposes of this question, Y is not considered a consonant
a =
Since order is not important, then this is a combination.
First find the total number of combinations of 4 letters chosen from RANDOMLY.
We chose 4 items from 8 objects: \(^{8}C_4=\frac{8!}{4!4!}=70\)
Now find the number of combinations of 4 letters chosen from the consonants RNDMLY
We chose 4 items from 6 objects: \(^{6}C_4=\frac{6!}{4!2!}=15\)
The probability that all letters chosen are consonants = \(\frac{15}{70}\)

The Barcelona soccer team includes 1 goalkeeper, 4 defenders, 3 midfielders and 3 attackers.
The manager has a squad of 22 players to choose from: 3 goalkeepers, 8 defenders, 6 midfielders and 5 attackers.
In how many ways can the Barcelona manager pick the team of 11 players?
Number of different teams =
We choose 1 item from 3: \(^{3}C_1=3\)
We choose 4 items from 8: \(^{8}C_4=70\)
We choose 3 items from 6: \(^{6}C_3=20\)
We choose 3 items from 5: \(^{5}C_3=10\)
There are 3 x 70 x 20 x 10 = 42 000 ways
A history exam has 2 sections. Section A has 5 questions and section B has 3 questions.
A student must answer 3 questions.
How many different ways are there of selecting 3 questions if a student must answer at least one question from each section?
Number of ways =
The student could either answer:
2 section A questions and 1 section B question
= \(^{5}C_2\cdot^{3}C_1=10\times3=30\)
or
1 section A question and 2 section B questions
= \(^{5}C_1\cdot^{3}C_2=5\times3=15\)
There are 30 + 15 = 45 ways in total
From a class of 8 boys and 8 girls, a group of 6 students is chosen for a quiz team. The team must have an even number of boys and girls. Donald has narcissistic tendencies and thinks he knows more than everyone else.
In how many ways can the team be selected if Donald (a boy) must be in the team?
Number of teams =
There must be 3 girls:
We choose 3 items from 8: \(^{8}C_3=56\)
There must be Donald:
There is only one Donald
There must be 2 more boys
We choose 2 items from 7: \(^{7}C_2=21\)
There are 56 x 1 x 21 = 1176
text

A team of five players is chosen from six males and 5 females.
- Determine how many different teams can be formed.
- Determine how many different teams can be formed consisting of 3 males and 2 females.
- Determine how many different teams can be formed if the team consists of more females than males
Hint
c. The team of 5 needs to contain more females than males.
It could have:
3 females and 2 males
Or
4 females and 1 male
Or
5 females and 0 males
Full Solution
Print from here

A five-digit number is formed by using the digits 1-5 exactly once.
- How many five-digit numbers are there?
- How many of these five-digit numbers are even?
Hint
For the digits 1-5, the number must end in 2 or 4.
How many arrangements end with 2?
How many arrangements end with 4?
Full Solution
Print from here

Seven students are placed at random in a line.
- How many different arrangements are there?
- What is the probability that the two youngest students are separated?
Hint
Treat the two youngest students as one object.
Consider finding the probability that the two youngest students are together.
Full Solution
Print from here
How much of Counting Principles have you understood?
Feedback
Which of the following best describes your feedback?



 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn