


On this page, you should learn to
- Use the nth term of a geometric sequence
- Use the nth term of a geometric series
- Use \(\sum\) notation for sums
- Understand applications such as compound interest and depreciation
- Find the sum of an infinite convergent series
The following videos will help you understand all the concepts from this page
Due to the style of the IB questions, it is not good to become reliant on the formula in the booklet. In the following video, we will gain a conceptual understanding of where the formula for the nth term of geometric sequences come from.
Notes from the video
Print from here
In the following applet, you can explore the effect changing r (and U1) has on the sequence.
What happens when
- r > 1
- r = 1
- 0 < r < 1
- r = 0
- -1 < r < 0
- r = -1
- r < -1
Being reliant on the formula for the nth term of a sequence can sometimes make the problems more difficult to solve. In the following video, it is far easier just to think about the problem conceptually.
A geometric sequence has second term 36 and fourth term 16.
Find the first term.
Notes from the video
Print from here
In the following video, we look at an example in which we have to find the number of terms in a geometric sequence. This requires us to solve an equation with indices. There are several ways of doing this: using logarithms, the table function on our calculator or a graphical method. The example is about compound interest.
$10 000 is invested in a bank receiving 4% interest at the end of each year.
How long does it take before the investment doubles in value?
Notes from the video
Print from here
In the following video, we need to use our algebraic skills to find an unknown
\(2k+5 \ ,\ k+5 \ ,\ k-1\) are consecutive terms of a geometric sequence. Find k
Notes from the video
Print from here
When we add terms of a sequence together, we call it a series
geometric sequence 1 , 2 , 4 , 8
geometric series 1 + 2 + 4 + 8
There are two formulae for the sum to n terms of a geometric series
\({ S }_{ n }=\frac { { U }_{ 1 }({ r }^{ n }-1) }{ r-1 } \) ... useful when r > 1
\({ S }_{ n }=\frac { { U }_{ 1 }({ 1-r }^{ n }) }{ 1-r } \) ... useful when r < 1
Sum to Infinity
If -1 < r < 1 , then the series is convergent
Here, r = 0.5 and the series converges.
When the series converges, we can find the sum to infinity
\({ S }_{ \infty }=\frac { { U }_{ 1 } }{ r-1 } \)
In the following video, we look at a typical exam-style question which involves the sum of a geometric series. In particular, we look at a very useful technique for solving simultaneous equations:
The sum of the first three terms of a geometric series is 61.
The sum to infinity is 125.
Find the common ratio.
Notes from the video
Print from here
Here is a quiz that practises the skills from this page
START QUIZ!
Geometric Sequence 1/1
The sequence below are either are arithmetic, geometric or neither. Drag the correct names into the spaces
geometric arithmetic neither geometric arithmetic neither geometric arithmetic neither geometric arithmetic neither geometric
1 , 4 , 7 , 10 , ...
1 , 2 , 4 , 8 , ...
0.5 , 1.25 , 2 , 2.75 , ...
\(16 \ , \ 12 \ , \ 9 \ , \ \frac{27}{4} \ ,\ ...\)
1 , 1 , 2 , 3 , ...
2 , -6 , 18 , -54 , ...
1 , -1 , 1 , -1 ...
1 , 4 , 9 , 16 , ...
5 , -5 , -15 , -25 , ...
-1 , 0.1 , -0.01 , 0.001 , ...
1 , 4 , 7 , 10 , ... common difference, d = 3
1 , 2 , 4 , 8 , ... common ratio , r = 2
0.5 , 1.25 , 2 , 2.75 , ... common difference, d = 0.75
\(16 \ , \ 12 \ , \ 9 \ , \ \frac{27}{4} \ ,\ ...\) common ratio , r = \(\frac{12}{16}=\frac{9}{12}= \frac{\frac{27}{4}}{9}=\frac{3}{4}\)
1 , 1 , 2 , 3 , ... There is no common difference, there is no common ratio. It is the Fibonacci sequence.
2 , -6 , 18 , -54 , ... common ratio , r = -3
1 , -1 , 1 , -1 ... common ratio , r = -1
1 , 4 , 9 , 16 , ... There is no common difference, there is no common ratio. It is the sequence of square numbers.
5 , -5 , -15 , -25 , ... common difference, d = -10
-1 , 0.1 , -0.01 , 0.001 , ... common ratio , r = -0.1
Find the common ratio in the following geometric sequence
25 , 15 , 9 , ...
Write your answer as a fraction in it simplest form: \(\frac {a}{b}\)
a =
b =
25 , 15 , 9 , ...
\(r = \frac {15}{25}=\frac {9}{15}=\frac {3}{5}\)
Find the common ratio in the following geometric sequence
6 , -3 , 1.5 , ...
Write your answer as a decimal
r =
6 , -3 , 1.5 , ...
\(r = \frac {-3}{6}=\frac {1.5}{-3}=-0.5\)
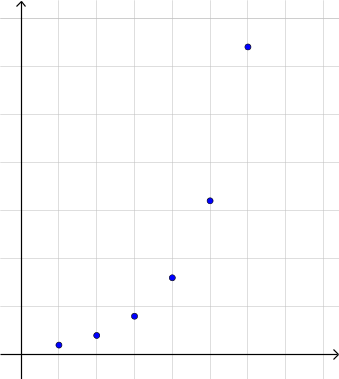
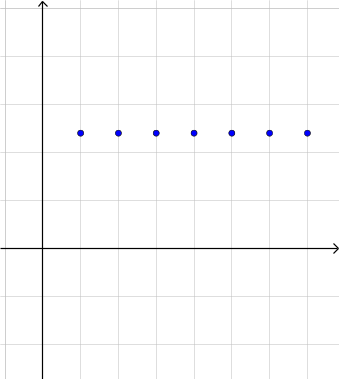
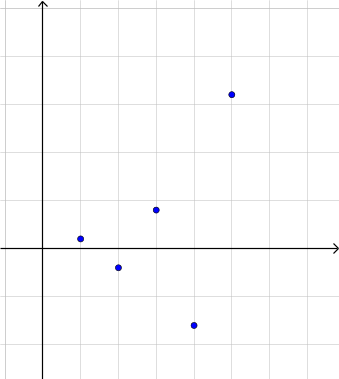
The following 5 graphs are visual representations of different geometric sequences. What is the value of r , the common ratio for each one?
r = 0 r = 1 r = 0.5 r = 2 r = -2 r = -0.5
|
|
|
|
|
The following is a geometric sequence. Fill in the gaps
5 , , , 40
Common ratio = 2
5 , 10 , 20 , 40
The following is a geometric sequence. Fill in the gaps
, , 8 , \(-\frac {16}{3}\)
Common ratio = \(-\frac {2}{3}\)
18 , -12 , 8 , \(-\frac {16}{3}\)
The first two terms of a geometric sequence are 4 , -8
\(U_{10}= a \times (-2)^{b}\)
Find a and b
a =
b =
\(U_{n}= U_{1} \times (r)^{n-1}\)
U2 and U5 are terms of a geometric sequence.
U2 = 9
U5 = -243
Find the terms below
U1 =
U8 =
_ , 9 , _ , _ , -243
\(9 \times r^3 = -243 \\ \quad \ r^3 = \frac {-243}{9} \\ \quad \ r^3 = -27\\ \quad \ r = \sqrt [ 3 ]{ -27 } \\ \quad \ r = -3 \)
-3 , 9 , -27 , 81 , -243 , 729 , -2187 , 6561
Find the sum of the first 6 terms of the following sequence
1.5 , 3 , 6 , ...
sum =
This is a geommetric sequence with
U1 = 1.5
r = 2
n = 6
\({ S }_{ n }=\frac { { U }_{ 1 }\left( { r }^{ n }-1 \right) }{ r-1 } \\ { S }_{ 6 }=\frac { 1.5\left( { 2 }^{ 6 }-1 \right) }{ 2-1 } \\ { S }_{ 6 }=\frac { 1.5\times 63 }{ 1 } \\ { S }_{ 6 }= 94.5\)
The first term of a geometric series is 10.
The sum to infinity is 50
Find U2
U2 =
\({ S }_{ \infty }=\frac { { U }_{ 1 } }{ 1-r } \\ 50 = \frac { 10 }{ 1-r } \\ 1-r = \frac { 10 }{ 50 } \\ 1-r = \frac { 1 }{ 5 } \\ r = \frac { 4 }{ 5 } \\\)
\(10\div \frac { 4 }{ 5 } =8\)
Here is a quiz about the financial applications of geometric sequences
START QUIZ!
Financial Applications of geometric sequences 1/1
$5 000 is invested in a fixed deposit account with annual interest rate of 3% compounded annually. Calculate the value of the investment after 8 years.
Give your answer to the nearest dollar
Value of investment = $
\(\large5000 \times (1+\frac{3}{100})^8\\\large =6\ 333.85\\\large =$6\ 334\)
$7 500 is invested in a fixed deposit account with annual interest rate of 1.6% compounded quarterly. Calculate the value of the investment after 5 years.
Give your answer to the nearest dollar
Value of investment = $
\(\large7500 \times (1+\frac{1.6}{4\times100})^{5\times4}\\\large =8\ 123.36\\\large =$8\ 123\)
€ 2 500 is invested in a fixed deposit account with annual interest rate of 2.4% compounded monthly. Calculate the value of the investment after 4 years.
Give your answer to the nearest euro
Value of investment = €
\(\large2500 \times (1+\frac{2.4}{12\times100})^{4\times12}\\\large =2\ 751.63\\\large =€2\ 752\)
€ 800 is invested in a fixed deposit account with annual interest rate of 5.8% compounded half-yearly. Calculate the value of the interest received after 10 years.
Give your answer to the nearest euro
Value of interest = €
\(\large800 \times (1+\frac{5.8}{2\times100})^{10\times2}-800\\\large =617.09\\\large =€617\)
A Tesla 3 is purchased in September 2021 for $43 990. If it depreciates in value by 12% per year, calculate the value of the car in September 2025.
Give your answer to the nearest dollar

Value of car = $
\(\large43\ 990 \times (1-\frac{12}{100})^4\\\large =26\ 380.60\\\large =$26\ 381\)
A Mercedes S Class is purchased for €100 600. How many years will it take for the value of the car to fall below €50 000 if it depreciates in value by 9% per year.

After years
After n years, value = \(\large100 \ 600 \times (1- \frac{9}{100})^n\)
After 7 years, value = 51 986
After 8 years, value = 47 307
Amir invests some money in an account that pays an annual interest rate of 4% that is compounded half-yearly.
The amount of money in Amir's account at the end of the year follows a geometric sequence with a commmon ratio r.
Find the value of r (give the exact value)
r =
\(\large (1+ \frac{4}{2\times100})^2=1.0404\)
On 1st January 2022, Aaliyah invests some money in an account that pays an annual interest rate of 4% that is compounded quarterly.
Find the year in which the amount of money in the account has doubled in value.
Year =
If $P is invested, the value of the investment after n years
\(\large P \times (1+\frac{4}{4\times100})^{4n}\\\large =P\times 1.01^{4n} \)
We want to find the number of years before the investment has a value of $2P
We need to solve
\(\large 2P=P\times 1.01^{4n} \\\large2=1.01^{4n}\)
We can solve by trial and error or using logarithms
\(\large \log 2=\log{1.01}^{4n}\\ \large \log 2=4n\log{1.01}\\ \large \frac{\log2}{\log1.01}=4n\\ \large4n=69.7\\ \large n=17.4\)
Hence, it will take 18 years.
2022 + 18 = 2040
$P is invested in a fixed deposit account with annual interest rate of 5% compounded quarterly. The value of the investments after 8 years is $5208 . What was the initial amount invested?
Give your answer to the nearest dollar
Initial investment = $
\(\large5\ 208=P \times (1+\frac{5}{4\times100})^{8\times 4}\\ \large5\ 208=P \times 1.0125^{32}\\ \large \frac{5 \ 208}{1.0125^{32}}=P\\ \large P =3\ 499.69\\\large P=$3\ 500\)
A sum of money is invested in a fixed deposit account with annual interest rate of r% compounded monthly. If the investment doubles in value after 10 years, find the rate of interest, r
Give your answer to the nearest whole number
r = %
If P is invested, we are trying to find the rate of interest that will make the value be 2P after 10 years.
We need to solve
\(\large2P=P \times (1+\frac{r}{12\times100})^{10\times12}\\\)
We can see that the value of the initial investment is irrelevant. We need to solve
\(\large2= (1+\frac{r}{12\times100})^{10\times12}\\ \large 2= (1+\frac{r}{1200})^{120}\\ \large \sqrt[120]{2}=1+\frac{r}{1200}\\ \large (\sqrt[120]{2}-1)\times1200=r\\ \large r=6.95\\ \large r=7\)
text


The nth term of a geometric sequence is Un , where Un =\(48(\frac{1}{4})^n\)
a) Find U1
b) Find the sum to infinity of the series
Hint
a) let n = 1
b) \({ S }_{ \infty }=\frac { { U }_{ 1 } }{ 1-r } \)
Full Solution
Print from here


The first term of a geometric series is 10. The sum to infinity is 50.
a) Find the common ratio
The nth term is Un
b) Find the value of \(\sum _{ n=1 }^{ 20 }{ { U }_{ n } } \)
Hint
a) \({ S }_{ \infty }=\frac { { U }_{ 1 } }{ 1-r } \)
b) You can use your graphical calculator to find the sum
Full Solution
Print from here


Three terms of a geometric sequence are \(x+6 \ , \ 12 \ ,\ x-1\)
Find the possible values of x
Hint
Full Solution
Print from here


Consider the geometric sequence where the first term is 45 and the second term is 36.
a) Find the least value of n such that the nth term of the sequence is less than 1
b) Find the least value of n such that the sum of the first n terms of the sequence is more than 200.
c) Find the sum to infinity.
Hint
You can make good use of your calculator to solve the inequalties in part a and b.
Full Solution
Print from here


The sum to infinity of a geometric series is 27.
The sum of the first 3 terms is 19.
Find the common ratio
Hint
We need to solve simultaneous equations.
Notice that \(\frac { { U }_{ 1 } }{ 1-r } \) is common to both equations
Full Solution
Print from here


The 2nd, 3rd and 6th terms of an arithmetic sequence with common difference \(d, \ d\neq 0\) form the first three terms of a geometric sequence, with common ratio, r.
The 1st term of the arithmetic sequence is -2.
a) Find d.
The sum of the first n terms of the geometric sequence exceeds the sum of the first n terms of the arithmetic sequence by at least 1000.
b) Find the least value of n for which this occurs.
Hint
a) Geometric sequence is U2 , U3 , U6
b) You can make good use of the table function on your graphical calculator to solve
(sum to n terms of geometric sequence) - (sum to n terms of arithmetic sequence) > 1000
Full Solution
Print from here


U1 = cosx ,U2 = sin2x are the first two terms of a geometric sequence, \(-\frac{\pi}{2}<x<\frac{\pi}{2}\)
a) Find U3 in terms of cosx
b) Find the set of values of x for which the geometric series converges
Hint
a) \(sin2x\equiv 2sinxcosx\)
b) For a series to converge -1 < r < 1
Full Solution
Print from here


a) Jessica takes out a loan of $200 000 to buy an appartment. The interest rate is 4% and is calculated at the end of each year. Calculate to the nearest dollar the amount Jessica would owe the bank after 15 years.
b) In order to pay of the loan, she pays $P into a bank at the end of each year. She receives an interest rate of 2.5% per year. Find the amount saved after 15 years.
c) What must be the value of P so that she has saved enough money to pay off the loan.
Hint
a) This is a geometric sequence
b) This is a geometric series
c) In order to pay of the loan
Amount of savings = Amount of loan
Full Solution
Print from here
How much of Geometric Sequences have you understood?
Feedback
Which of the following best describes your feedback?


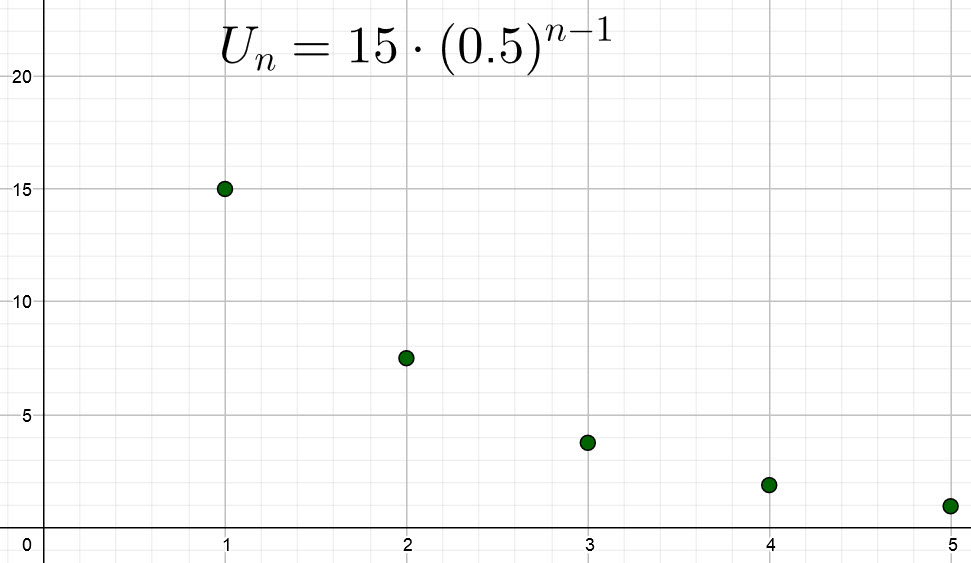



 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn