Here is a quiz that will test your basic understanding of logarithms
Work out
\(\large\log_28=\)
From the definition of logs, we know that
\(\large\log_ab=x \ \Leftrightarrow \ a^x=b\)
\(\large 2^3=8\)
Work out
\(\large\log_381=\)
From the definition of logs, we know that
\(\large\log_ab=x \ \Leftrightarrow \ a^x=b\)
\(\large 3^4=81\)
Work out
\(\large\log_{10}0.1=\)
From the definition of logs, we know that
\(\large\log_ab=x \ \Leftrightarrow \ a^x=b\)
\(\large 10^{-1}=\frac{1}{10^1}=0.1\)
Work out
\(\large\log_42=\)
Give your answer as a decimal
From the definition of logs, we know that
\(\large\log_ab=x \ \Leftrightarrow \ a^x=b\)
\(\large 4^{0.5}=\sqrt{4}=2\)
Work out
\(\large\log_{100}\sqrt{100}=\)
Give your answer as a decimal
From the definition of logs, we know that
\(\large\log_ab=x \ \Leftrightarrow \ a^x=b\)
\(\large 100^{0.5}=\sqrt{100}\)
Work out
\(\large\log_a\frac{1}{\sqrt{a}}=\)
Give your answer as a decimal
From the definition of logs, we know that
\(\large\log_ab=x \ \Leftrightarrow \ a^x=b\)
\(\large a^{-0.5}=\frac{1}{a^{\frac{1}{2}}}=\frac{1}{\sqrt{a}}\)
Work out
\(\large\log_aa^3=\)
From the definition of logs, we know that
\(\large\log_ab=x \ \Leftrightarrow \ a^x=b\)
Work out
\(\large\log_48=\)
Give your answer as a decimal
From the definition of logs, we know that
\(\large\log_ab=x \ \Leftrightarrow \ a^x=b\)
\(\large 4^{\frac{3}{2}}=(\sqrt{4})^3=2^3=8\)
From the definition of logs, we know that
\(\large\log_ab=x \ \Leftrightarrow \ a^x=b\)
\(\large 10^0=1\)
Work out
\(\large\log_4\frac{1}{2}=\)
Give your answer as a decimal
From the definition of logs, we know that
\(\large\log_ab=x \ \Leftrightarrow \ a^x=b\)
\(\large 4^{-\frac{1}{2}}=\frac{1}{4^{\frac{1}{2}}}=\frac{1}{\sqrt{4}}=\frac{1}{2}\)
Here is a quiz about the laws of logarithms
If \(\large\log2+\log5=\log a\)
Work out a
From the fomula booklet, we know the following about logs
\(\large\log_axy=\log_ax+\log_ay\)
In this case,
\(\large\log2+\log5=\log (2\times5)\)
If \(\large\log3+\log4=\log a\)
Work out a
From the fomula booklet, we know the following about logs
\(\large\log_axy=\log_ax+\log_ay\)
In this case, \(\large\log3+\log4=\log (3\times4)\)
If \(\large\log15-\log3=\log a\)
Work out a
From the fomula booklet, we know the following about logs
\(\large\log_a\frac{x}{y}=\log_ax-\log_ay\)
In this case, \(\large\log15-\log3=\log (\frac{15}{3})=\log5\)
If \(\large\log20-\log2-\log5=\log a\)
Work out a
From the fomula booklet, we know the following about logs
\(\large\log_a\frac{x}{y}=\log_ax-\log_ay\)
In this case, \(\large\log20-\log2-\log5=\log (20\div2)-\log5=\log(10\div5)=\log2\)
If \(\large2\log3=\log a\)
Work out a
From the fomula booklet, we know the following about logs
\(\large\log_ax^m=m\log_ax\)
In this case, \(\large2\log3=\log 3^2\)
If \(\large3\log2=\log a\)
Work out a
From the fomula booklet, we know the following about logs
\(\large\log_ax^m=m\log_ax\)
In this case, \(\large3\log2=\log 2^3\)
If \(\large a\log3=\log 81\)
Work out a
From the fomula booklet, we know the following about logs
\(\large\log_ax^m=m\log_ax\)
In this case, \(\large \log 81=\log 3^4=4\log3\)
If \(\large2\log4-0.5\log16=0.5\log a\)
Work out a
From the fomula booklet, we know the following about logs
\(\large\log_a\frac{x}{y}=\log_ax-\log_ay\)
\(\large\log_ax^m=m\log_ax\)
In this case,
\(\large2\log4-0.5\log16=\log4^2-\log\sqrt{16}=\log16-\log4=\log12\)
\(\large\log12=0.5\log144\)
Solve for x
\(\large\log_2(2x+4)-\log_2(x-1)=3\)
From the fomula booklet, we know the following about logs
\(\large\log_a\frac{x}{y}=\log_ax-\log_ay\)
In this case,
\(\large\log_2(2x+4)-\log_2(x-1)=\log_2\frac{2x+4}{x-1}\)
Therefore,
\(\large\log_2\frac{2x+4}{x-1}=3\)
\(\large\frac{2x+4}{x-1}=2^3\\
\large\frac{2x+4}{x-1}=8\\\)
Solve the equation
\(\large 2x+4=8(x-1)\\
2x+4=8x-8\\
12=6x\\
x=2\)
Solve for x
\(\large\log4x-\log(x-3)=1\)
From the fomula booklet, we know the following about logs
\(\large\log_a\frac{x}{y}=\log_ax-\log_ay\)
In this case,
\(\large\log4x-\log(x-3)=\log\frac{4x}{x-3}\)
We have \(\large\log\frac{4x}{x-3}=1\)
Remember that \(\large \log\) means \(\large \log_{10}\)
Therefore,
\(\large\frac{4x}{x-3}=10^1\)
Solve the equation
\(\large 4x=10(x-3)\\
4x=10x-30\\
30=6x\\
x=5\)
Here is a quiz that tests your knowledge of changing bases of logarithms
If \(\large \log_27=\frac{\log a}{\log b}\)
work out a b
The change of base formula from the formula booklet is useful here
\(\large \log_ax=\frac{\log_bx}{\log_ba}\)
If \(\large \log3=\frac{\log_2a}{\log_2b} \)
work out a b
The change of base formula from the formula booklet is useful here
\(\large \log_ax=\frac{\log_bx}{\log_ba}\)
Remember that \(\large \log\) means \(\large \log_{10}\)
If \(\large \log_35=\frac{\log_6a}{\log_b3}\)
work out a b
The change of base formula from the formula booklet is useful here
\(\large \log_ax=\frac{\log_bx}{\log_ba}\)
In this case,
\(\large \log_35=\frac{\log_65}{\log_63}\)
If \(\large \log_ab=\frac{\log 8}{\log 4}\)
work out a b
The change of base formula from the formula booklet is useful here
\(\large \log_ax=\frac{\log_bx}{\log_ba}\)
If \(\large \log_a5=\frac{\log_25}{3}\)
work out a
The change of base formula from the formula booklet is useful here
\(\large \log_ax=\frac{\log_bx}{\log_ba}\)
We use this
\(\large 3=\log_28\)
and so
\(\large \log_85=\frac{\log_25}{\log_28}\)
Work out a b
\(\large -\log_ab=\frac{\log \frac{1}{5}}{\log 3}\)
The change of base formula from the formula booklet is useful here
\(\large \log_ax=\frac{\log_bx}{\log_ba}\)
\(\large -\log_ab=\log_a{b^{-1}}=\log_a{\frac{1}{b}}=\frac{\log \frac{1}{b}}{\log a}\) Therefore,
\(\large \frac{\log \frac{1}{b}}{\log a}=
\frac{\log \frac{1}{5}}{\log 3}\)
Work out a b
\(\large \frac{\log 0.25}{\log 8}=-\log_ab\)
The change of base formula from the formula booklet is useful here
\(\large \log_ax=\frac{\log_bx}{\log_ba}\)
\(\large \frac{\log 0.25}{\log 8}=\log_80.25\)
And,
\(-\log_80.25=\log_8(\frac{1}{4})^{-1}=\log_84\)
If \(\large \log_{5^2}3^5=\frac{5\log 3}{a\log b}\)
work out a b
The change of base formula from the formula booklet is useful here
\(\large \log_ax=\frac{\log_bx}{\log_ba}\)
\(\large \log_{5^2}3^5=\frac{\log 3^5}{\log 5^2}=\frac{5\log 3}{2\log 5}\)
If \(\large \log_2x=\log_x2\)
work out 2 possible values of x
Put values in order of size
The change of base formula from the formula booklet is useful here
\(\large \log_ax=\frac{\log_bx}{\log_ba}\)
In this case, we can write the right-hand side of the equation in terms of log base 2
\(\large \log_x2=\frac{\log_22}{\log_2x}=\frac{1}{\log_2x}\)
Our equation becomes
\(\large \log_2x=\frac{1}{\log_2x}\\
\large(\log_2x)^2=1\\
\log_2x=\pm1\)
\(\large x=2^1 \) or \(\large x=2^{-1} \)
Solve for x
\(\large \log_2x-1=\log_4x\)
The change of base formula from the formula booklet is useful here
\(\large \log_ax=\frac{\log_bx}{\log_ba}\)
In this case, we can write the right-hand side of the equation in terms of log base 2
\(\large \log_4x=\frac{\log_2x}{\log_24}=\frac{\log_2x}{2}\)
Our equation becomes
\(\large \log_2x-1=\frac{\log_2x}{2}\\
\large 2(\log_2x-1)=\log_2x\\
\large 2\log_2x-2=\log_2x\\
\)
Rearrange the equation
\(\large 2\log_2x-\log_2x=2\\
\large \log_2x=2\\x=2^2\)
Here is a quiz about solving index equations. You will not need to use logarithms to solve all of these.
Solve for x
\(\large 2^x=8\)
Solve for x
\(\large 4^{-x}=2\)
Write your answer as a decimal
Write 4 as a power of 2
\(\large 4^{-x}=(2^2)^{-x}\)
The index equation becomes
\(\large 2^{-2x}=2^1\)
Therefore,
-2x = 1
x = -0.5
Solve for x
\(\large 3^x=\frac{1}{27}\)
\(\large 3^x=\frac{1}{27}\\
\large 3^x=\frac{1}{3^3}\\
\large 3^x=3^{-3}\)
Solve for x
\(\large 16^x=64\)
Write your answer as a decimal
6 and 64 as powers of 4 (or 2)
\(\large 16=4^2 \ , \ 64=4^3\)
The equation becomes
\(\large (4^2)^x=4^3\\
2x=3 \\
x=1.5\)
Solve for x
\(\large 5^{x+2}=\frac{1}{25}\)
Write the right-hand side of the equation in terms of a power of 5
\(\large 5^{x+2}=\frac{1}{5^2}\\
\large 5^{x+2}=5^{-2}\\
\)
Now we can equate the powers
x+2 = -2
Solve for x
\(\large4^{x-2}=\frac{1}{2}\)
Write your answer as a decimal
Re-write the equation as powers of 2
\(\large4^{x-2}=\frac{1}{2}\\
\large(2^2)^{x-2}=2^{-1}\\
\large2^{2x-4}=2^{-1}\)
Now we can equate the powers
2x - 4 = -1
Solve for x
\(\large 4^{x+1}=8^{x-2}\)
Re-write the equations as powers of 2
\(\large 4^{x+1}=8^{x-2}\\
\large (2^2)^{x+1}=(2^3)^{x-2}\\
\large 2^{2x+2}=2^{3x-6}\)
Now we can equate the powers
2x + 2 = 3x - 6
8 = x
The solution to
\(\large 5^x=2^{x+1}\)
can be written in the form \(\large x=\frac{2}{(\log_2a-1)}\)
Work out a
In order to solve this eqution, we have to take logs of both sides.
It is slightly easier if we take logs base 2
\(\large \log_2(5^x)=\log_2(2^{x+1})\)
From the fomula booklet, we know the following about logs
\(\large\log_ax^m=m\log_ax\)
Our equation becomes
\(\large x\log_25=(x+2)\log_22\\
\large x\log_25=(x+2)\times1\\
\large x\log_25=x+2\\
\large x\log_25-x=2\\
\large x(\log_25-1)=2\\
\large x=\frac{2}{(\log_25-1)}\\\)
The solution to
\(\large 3^{x+1}=8^{x-1}\)
can be written in the form \(\large x=\frac{1+\log_3a}{\log_3b-1}\)
Work out a b
In order to solve this eqution, we have to take logs of both sides.
It is slightly easier if we take logs base 3
\(\large \log_3(3^{x+1})=\log_3(8^{x-1})\)
From the fomula booklet, we know the following about logs
\(\large\log_ax^m=m\log_ax\)
Our equation becomes
\(\large (x+1)\log_33=(x-1)\log_38\\
\large x+1=(x-1)\log_38\\
\large x+1=x\log_38-\log_38\\
\large 1+\log_38=x\log_38-x\\
\large 1+\log_38=x(\log_38-1)\\
\large x=\frac{1+\log_38}{\log_38-1}\)
The solution to
\(\large 2\cdot3^x=4^{x-1}\)
can be written in the form \(\large x=\frac{a}{b-\log_23}\)
Work out a
In order to solve this eqution, we have to take logs of both sides.
It is slightly easier if we take logs base 2
\(\large \log_2(2\cdot3^x)=\log_2(4^{x-1})\\
\)
From the fomula booklet, we know the following about logs
\(\large\log_ax^m=m\log_ax\)
\(\large\log_axy=\log_ax+\log_ay\)
Our equation becomes
\(\large \log_22+ \log_2(3^x)=\log_2(4^{x-1})\\
\large 1+ x\log_23=(x-1)\log_24\\
\large 1+ x\log_23=(x-1)\times2\\
\large 1+ x\log_23=2x-2\\
\large 3= 2x-x\log_23\\
\large 3= x(2-\log_23)\\
\large x=\frac{3}{2-\log_23}
\)
Here is a quiz that practises ALL the skills from this page
Each of these logarithm equations has an equivalent index equation. Match them up!
Remember that logx means log10 x
Write the value of these logarithms
23 = 8 5-2 = \(\frac{1}{5^2}=\frac{1}{25}\) 40.5 = \(\sqrt{4}=2\) lne = loge e=1 <=>e1 =e ln1 = loge 1=0 <=>e0 =1
This question uses the three log laws:
loga + logb = logab
loga - log b = log\(\frac{a}{b}\)
\(\log _{ 3 }{ 5 } =\frac { \log _{ c }{ a } }{ \log _{ c }{ b } } \)
What are the values of a b
This question uses the change of base formula:
\(\log _{ b }{ a } =\frac { \log _{ c }{ a } }{ \log _{ c }{ b } } \)
Which is the correct answer to log5 10?
\(\log _{ 5}{ 10 } =\frac { \log _{ 10 }{ 10 } }{ \log _{ 10 }{ 5 } } =\frac {1 }{ \log { 5 } } \)
The first term of a geometric sequence is ln2 and the common ratio is 5.
What is the second term?
Second term = 5ln2 = ln25
Here is an arithmetic sequence
ln2 , U2 , ln50
What is the common difference, d U2
2d = ln50-ln2
2d = ln25
d = 0.5ln25
d = ln250.5
d = ln5
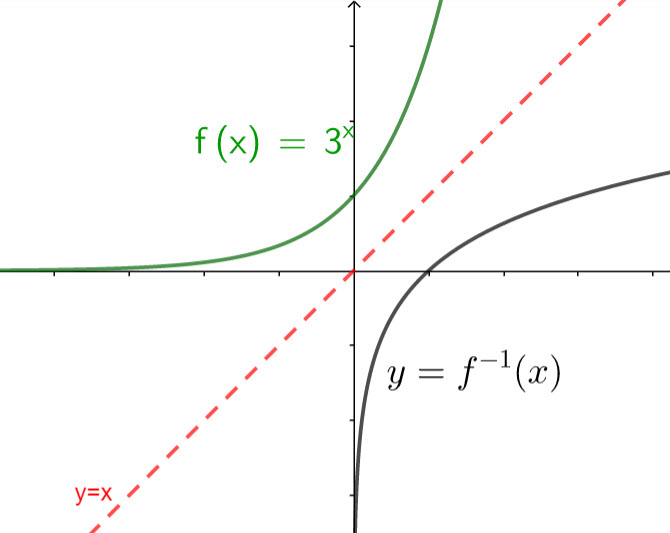
The graphs of y = f(x), y = x and y = f -1 (x) are plotted below, where f(x) = 3x
What is the function f -1 (x)?
The inverse of ax is loga x
The graph of y = log2 x is plotted below. What is the value of a
The solution to the equation 3x = 2x+1 can be written in the form \(\frac{log\ a}{log\frac{b}{c}}\)
Find a b c
3x = 2x+1
log3x = log2x+1
xlog3 = (x+1)log2
xlog3 = xlog2 = log2
xlog3 - xlog2 = log2
x(log3 - log2) = log2
x = \(\frac{log2}{log3-log2}\)
x = \(\frac{log2}{log\frac{3}{2}}\)













 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn