
The following page will help you with questions about the Binomial Theorem (or Binomial Expansion). The Binomial Theorem is used for expanding brackets in the form (a + b)n
On this page, you should learn to
- Expand \((a+b)^n\) using Pascal's triangle and \(^nC_r\)
The following videos will help you understand all the concepts from this page
Spotting the Pattern
At first look, the formula for the Binomial Theorem looks quite complicated
\(\left(a+b\right)^{n}=a^{n}+\left(\begin{array}{c} n\\ 1 \end{array}\right) a^{n-1}b+...+\left(\begin{array}{c} n\\ r \end{array}\right)a^{n-r}b^{r}+...+b^{n} \)
The formula is in the information booklet, so no need to try and lean it by heart! Applying it is not too difficult, but before we do that, it is important that we understand the pattern (or patterns) that lie behind it.
The following video shows you the patterns behind the Binomial Theorem
Print from here
Here is a short quiz to test your understanding of combinations
START QUIZ!
Here is a quiz that practises the Binomial expansion (a + b)n
START QUIZ!
How much of Binomial Theorem SL have you understood?


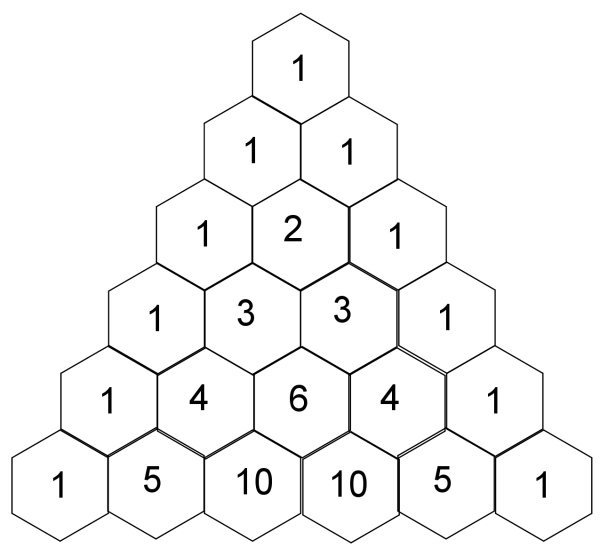
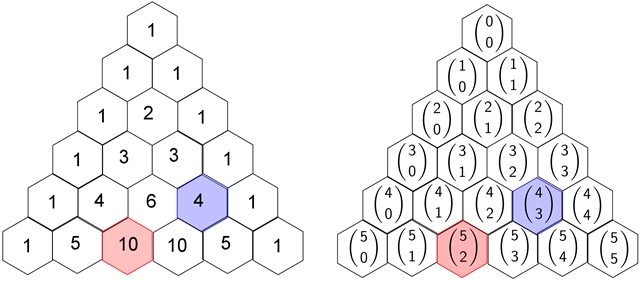
 Evaluate
Evaluate  Given that r>4, evaluate r , if
Given that r>4, evaluate r , if 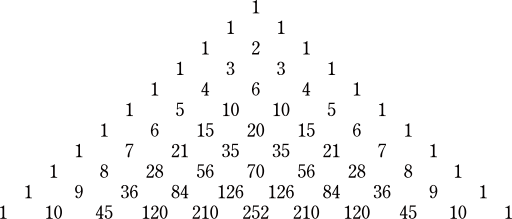








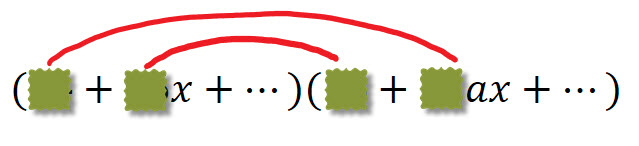

 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn