 This is a short topic. The Arrhenius equation is given in the data book in all its relevant forms so the important thing to do is to become familiar with the equation and to ensure that you know how to plot a graph using the Arrhenius equation in order to determine activation energy − this occasionally appears on examination papers.
This is a short topic. The Arrhenius equation is given in the data book in all its relevant forms so the important thing to do is to become familiar with the equation and to ensure that you know how to plot a graph using the Arrhenius equation in order to determine activation energy − this occasionally appears on examination papers.
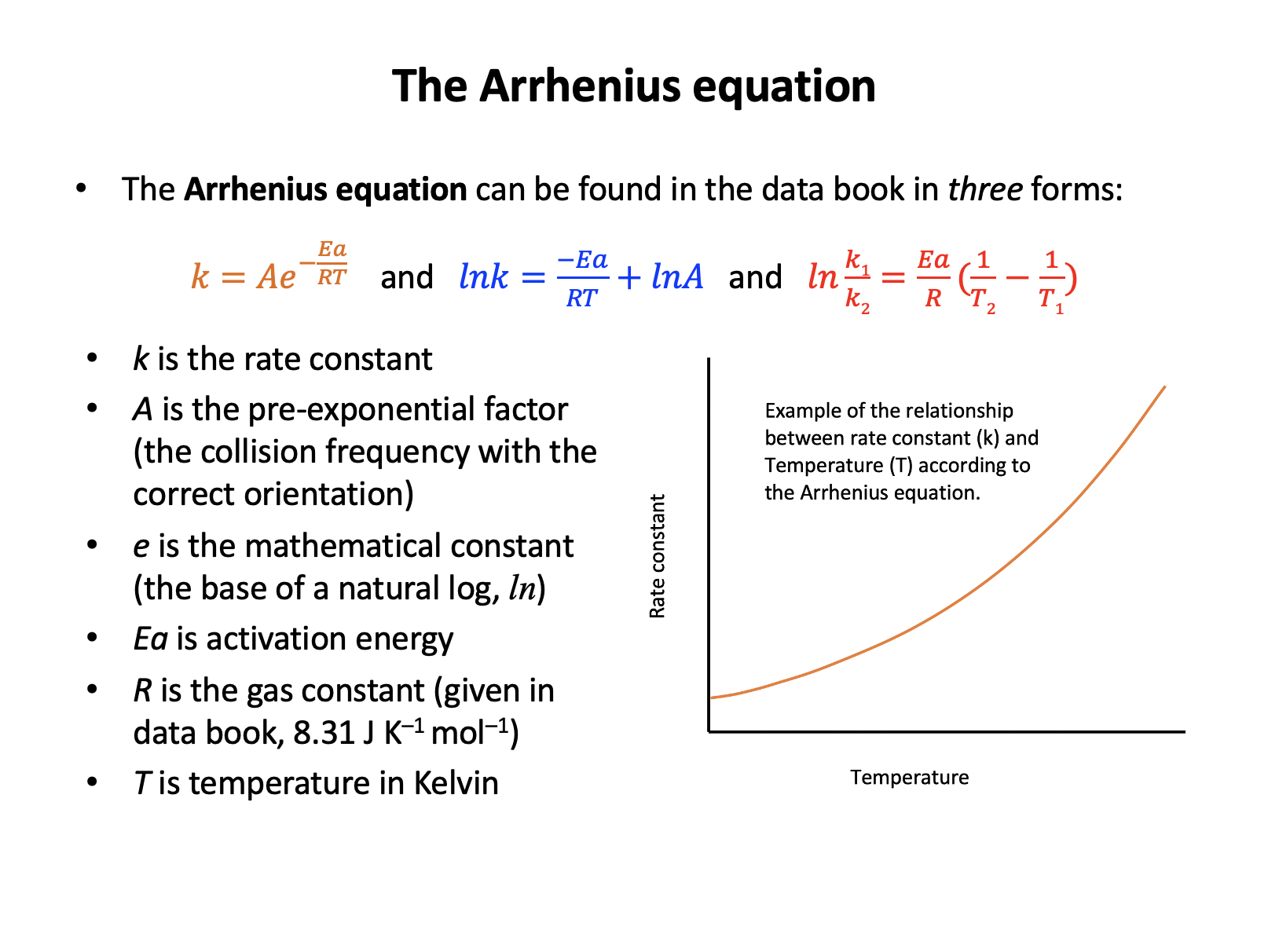
The Arrhenius equation is given in the data book:
\(k = Ae^{-E_a \over RT}\)
What happens to the value of the rate constant (k) if the temperature increases?
An increase in temperature will always increase the value of the rate constant (k is only constant at constant temperature). This can be shown by substituting values into the expression:
Using 40000J mol−1 for Ea and temperature of 298K.
\(e^{-E_a \over RT}\) = e−40000/(8.31×298) = 9.6 × 10−8
Using 40000J mol−1 for Ea and temperature of 308K.
\(e^{-E_a \over RT}\) = e−40000/(8.31×308)= 1.63 × 10−7
Assuming that Ea and A remain constant the increase in value of the 'e' expression must lead to an increase in the rate constant, k.
Thus the correct answer is 'The rate constant increases'.The Arrhenius equation is given in the data book:
\(k = Ae^{-E_a \over RT}\)
What does the pre-exponential factor, A, represent?
Taking natural logs of the Arrhenius equation gives the expression below:
\(ln k = {-E_a \over RT} + ln A\)
This can be used to determine the activation energy for a reaction because:
The equation given in the question can be compared to the equation for a straight line \(y = mx + c\):
\(ln k = {-E_a \over R}.{1 \over T} + ln A\)
The temperature term has been separated from the activation energy term, and this makes it easier to see that if y = lnk and x = 1/T then the gradient, m, will be –Ea/R and the intercept, c, will be lnA.
So the correct answer is Plotting a graph of 1/T against ln k is a linear plot with gradient equal to –Ea/R. The other answers are not correct as the expression has been incorrectly interpreted.
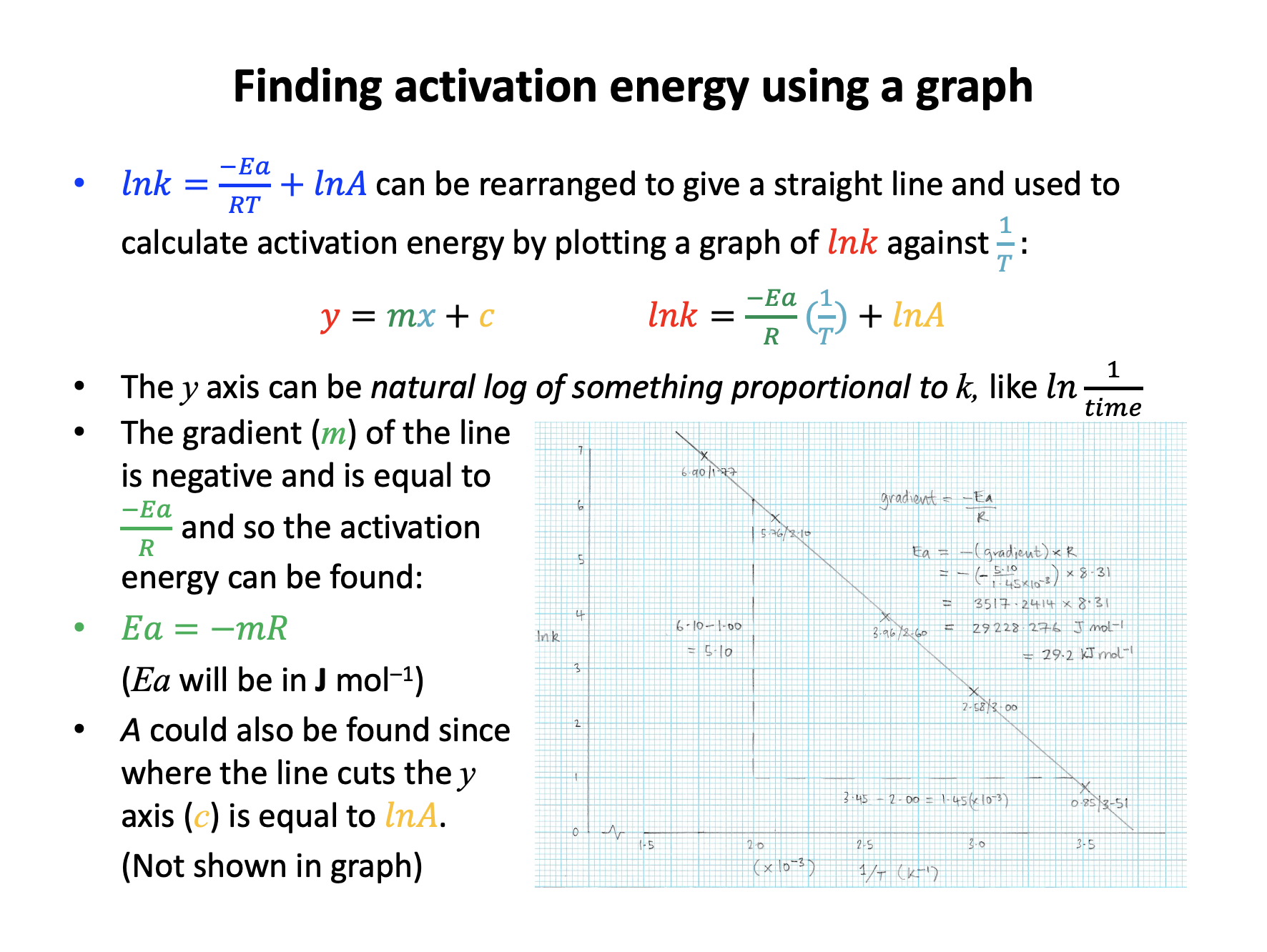
A student did an experiment to find the activation energy for a reaction that produced a precipitate. The student varied the temperature and measured how long it took for the precipitate to obsure a black cross written on a piece of white paper. The student collected results for 6 different temperatures, and drew a graph to calculate activation energy.
What should the student plot to find Ea?
The Arrhenius equation is given in the data book:
\(lnk = {-E_a \over RT} + lnA\)
and can be compared to the equation for a straight line \(y = mx + c\):
\(ln k = {-E_a \over R}.{1 \over T} + ln A\)
The temperature term has been separated from the activation energy term, and this makes it easier to see that if y = lnk and x = 1/T then the gradient, m, will be –Ea/R and the intercept, c, will be lnA.
It is important to remember that the rate constant is proportional to rate, and that rate is propotional to 1/time.
The expression lnk is the natural log of the rate constant, but because the activation energy is calculated from a gradient any value proportional to lnk can be plotted.
So the correct answer is 1/temperature against ln 1/time. The other answers are not correct as the expression has been incorrectly interpreted, or rate constant has been incorrectly correlated with time (rather than 1/time).
A student did an experiment to find the activation energy for a reaction that produced a precipitate. The student varied the temperature and measured how long it took for the precipitate to obsure a black cross written on a piece of white paper. The student collected results for 6 different temperatures, and drew a graph of 1/temperature (x axis) against ln 1/time (y axis) to calculate activation energy.
One result was that the reaction took 46 seconds (to obsure the cross) at a temperature of 40°C.
What values (2 sig figs) should the student use to plot this point on the graph?
For 1/T, remember that temperature must be in Kelvin:
40°C is 40+273=313K
1/313 = 0.003194888, which is 3.2 × 10–3 in standard form (2 sig figs)
For 1/t, don't forget to take the natural log (ln):
1/46 = 0.02173913
and ln 0.02173913 = –3.8
Thus 3.2 × 10–3 (x axis) and –3.8 (y axis) is the correct answer.
The incorrect answers: 1/40 = 0.025, which is 2.5 × 10–3 in standard form (not converted to Kelvin)
And 1/46 = 0.02173913 which is 2.2 × 10–2 in standard form (no natural log taken)
The Arrhenius equation, in the natural logarithmic form, is given in the data book:
\(lnk = {-E_a \over RT} + lnA\)
In an experiment studying the gas phase reaction of ethene and bromine at a temperature of 299K, the rate constant (k) was found to be 0.128 (mol–1 dm3 s–1) and the activation energy was found to be 40kJ mol−1.
What is the numerical value of the pre-exponential factor, A?
The activation energy must be converted to J (rather than kJ) since the gas constant R (given in the data book) has a value of 8.31 J K−1 mol−1. Ea = 40000 J mol−1.
ln0.128 = −40000/(8.31×299) + lnA
−2.055725015 = −16.09858775 + lnA
lnA = 14.04286274
A = e14.04286274 = 1255271.874
So the correct answer is 1.26 × 106 (3 dp)
Incorrect answers:
7.69 uses 40 rather than 40000
14.0 is the natural log of the answer (not converted to A)
2.04 is the natural log of the answer (not converted to A) using 40 rather than 40000
Paper 1
Core (SL&HL): Kinetics core (SL and HL) paper 1 questions
AHL (HL only): Kinetics AHL (HL only) paper 1 questions
Paper 2
Core (SL&HL): Kinetics core (SL & HL) paper 2 questions
AHL (HL only): Kinetics AHL (HL only) paper 2 questions
How much of Activation energy have you understood?








 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn