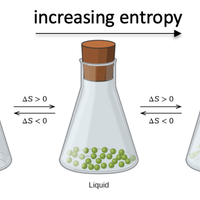
 According to the second law of thermodynamics, a process is spontaneous if it causes the total entropy of universe to increase. Entropy is a measure of the number of ways in which the energy in a system can be arranged. Use the practice questions to help you become more confident in predicting which systems have a positive entropy change. You should also be able to calculate the entropy change of a system using absolute entropy values.
According to the second law of thermodynamics, a process is spontaneous if it causes the total entropy of universe to increase. Entropy is a measure of the number of ways in which the energy in a system can be arranged. Use the practice questions to help you become more confident in predicting which systems have a positive entropy change. You should also be able to calculate the entropy change of a system using absolute entropy values.
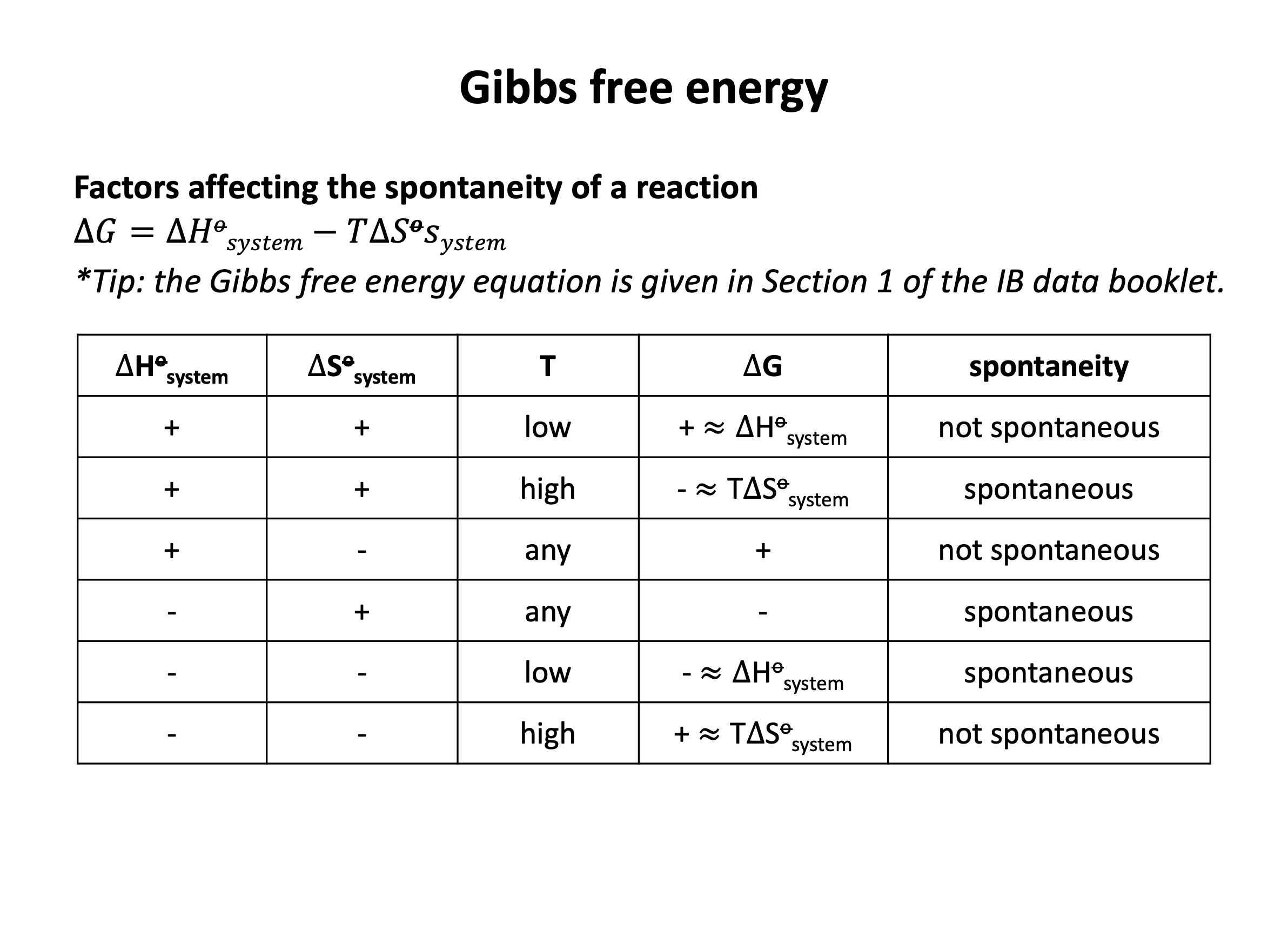
The Gibbs free energy change takes into account both the entropy change of the system and that of the surroundings, the latter a result of the reaction being either exothermic or endothermic. Gibbs free energy calculations are not difficult, but it is easy to trip up by forgetting to convert your entropy energy unit from J to kJ. Refer to revision card 18 to help you organise your working. You should also be able to predict the spontaneity of a process knowing the enthalpy change of the system, the entropy change of the system and the reaction temperature. Remember that a spontaneous reaction here refers to a reaction that is thermodynamically feasible and does not give any indication about the rate of the reaction.
Ensure you are confident using the terms below and learn the asterisked* definitions
Entropy, spontaneous, absolute entropy (So)*, Gibbs free energy change (ΔG), Gibbs free energy of formation (ΔGof)*
Which of the statements below is the best definition of entropy?
The best definition is A measure of the number of ways of arranging energy within particles and this is the correct answer.
Entropy is sometimes described as a 'measure of disorder', but this may be misleading and should be avoided.
'The change in heat energy at constant pressure' is a definition of Enthalpy change (ΔH). 'The average kinetic energy of a system' is a definition of temperature, T.
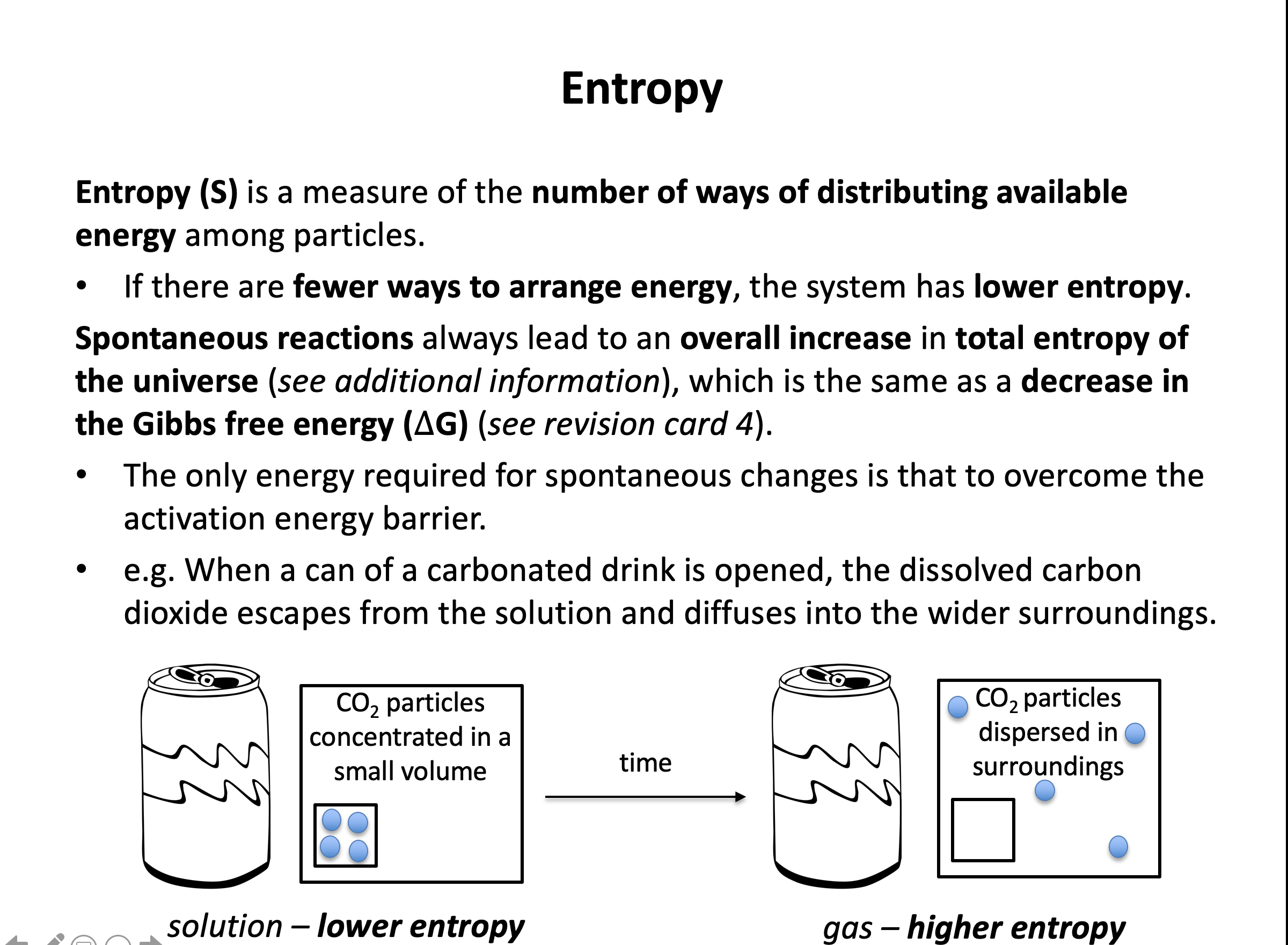
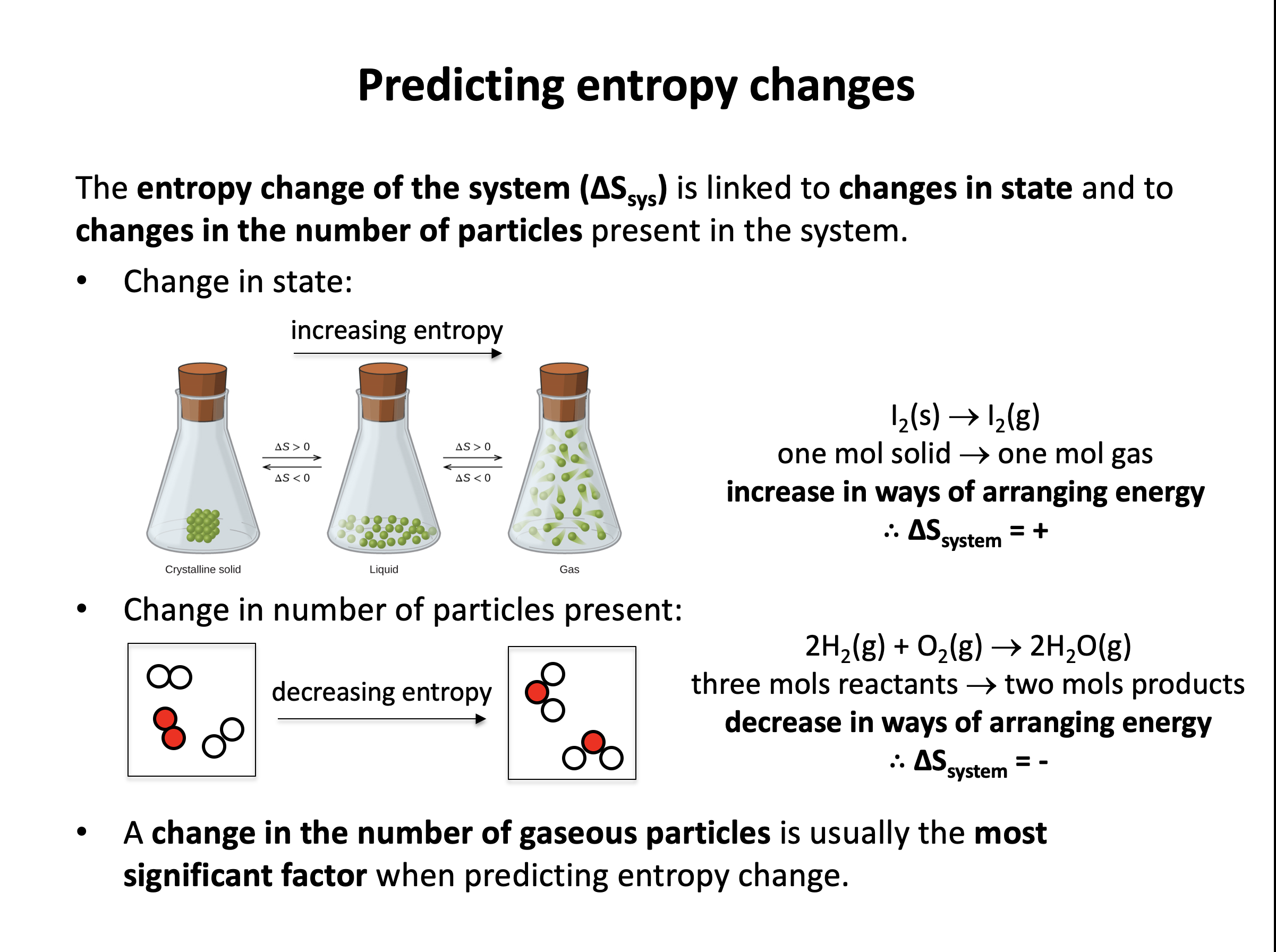
Which reaction has the greatest positive entropy change, ΔS (of the system).
Gases tend to have greater entropy than liquids (or solutions), that tend to have greater entropy than solids. Any change that leads to a greater number of gaseous moles tends to lead to an increase in the entropy of the system.
Thus the correct answer here is CaCO3(s) → CaO(s) + CO2(g)
The other reactions involve the creation of liquids or solids from gases, or a decrease in the number of gaseous moles.
Which reaction has the greatest positive entropy change, ΔS (of the system).
Gases tend to have greater entropy than liquids (or solutions), that tend to have greater entropy than solids. Any change that leads to a greater number of gaseous moles tends to lead to an increase in the entropy of the system.
Thus the correct answer here is CH4(g) + 1½O2(g) → CO(g) + 2H2O(g) since 2½ moles of gas react to give 3 moles of gas.
The other reactions involve the creation of liquid water rather than gaseous water, or no increase in the number of gaseous moles.
Which reaction has an entropy change, ΔS (of the system) that is closest to zero?
Gases tend to have greater entropy than liquids (or solutions), that tend to have greater entropy than solids. Any change that leads to a greater number of gaseous moles tends to lead to an increase in the entropy of the system.
Thus the correct answer is H2(g) + Cl2(g) → 2HCl(g) since 2 moles of gas react to give 2 moles of gas. So the entropy change of the system is likely to be very close to zero.
The other reactions involve the creation of liquid water from gaseous water (negative ΔS), a decrease in the number of gaseous moles (negative ΔS), or the creation of a gaseous product from a solid reactant (positive ΔS).
Calculator question: Using the standard entropy values from the data book (values given below), what is the standard entropy change ΔSo (in JK–1mol–1) of the system for the combustion of methane?
CH4(g) + 2O2(g) → CO2(g) + 2H2O(l)
Standard entropy values (ΔSo) in JK–1mol–1
CH4(g) +186.0 | O2(g) +205.0 | CO2(g) +213.8 | H2O(l) +70.0
The standard entropy change can be calculated by finding the difference between the standard entropy of the reactants and the standard entropy of the products; ΔS = S(products) – S(reactants).
The standard entropy of the reactants is 186 + 2×205.0 = 596.0
The standard entropy of the products is 213.8 + 2×70.0 = 353.8
Thus the standard entropy change is 353.8 – 596.0 = –242.2 (in JK–1mol–1) which is the correct answer.
Incorrect answers
+242.2 is obtained if ΔS is found by S(reactants) – S(products) instead of ΔS = S(products) – S(reactants).
–107.2 is obtained if one mole is used for every species in the calculation instead of using two moles of oxygen and two moles of water.
+107.2 is obtained if one mole is used for every species in the calculation instead of using two moles of oxygen and two moles of water and ΔS is found by S(reactants) – S(products) instead of ΔS = S(products) – S(reactants).
Calculator question: Using the standard entropy values from the data book (some values given below), what is the entropy change ΔS (in JK–1mol–1) of the system for the reaction as written below?
2H2(g) + O2(g) → 2H2O(g)
Standard entropy values (ΔSo) in JK–1mol–1
H2(g) +131.0 | O2(g) +205.0 | H2O(g) +188.8 | H2O(l) +70.0
The entropy change can be calculated by finding the difference between the standard entropy of the reactants and the standard entropy of the products; ΔS = S(products) – S(reactants).
The standard entropy of the reactants is 2×131.0 + 205.0 = 467.0
The standard entropy of the products is 2×188.8 = 377.6
Thus the standard entropy change is 377.6 – 467.0 = –89.4 (in JK–1mol–1) which is the correct answer.
Incorrect answers
–278.2 is obtained if one mole of water is used (products) instead of two moles of water.
–147.2 is obtained if one mole is used for every species in the calculation instead of using two moles of hydrogen and two moles of water.
–327 is obtained if the value used for water is liquid water (+70.0) instead of gaseous water (+188.8) as written in the equation.
For a chemical reaction to be thermodynamically spontaneous, which of the following must always be true?
For a reaction to be thermodynamically spontaneous the change in Gibb's free energy (ΔG) must be equal to or less than zero (there must be an overall gain in entropy in the universe). Since ΔG = ΔH−TΔS (this should be learned), the correct answer is ΔH−TΔS ≤ 0 since this is stating that ΔG ≤ 0.
Incorrect answers (refer to ΔG = ΔH−TΔS)
The reaction does not always have to be exothermic. (ΔH < 0 shows an exothermic reaction.) Exothermic reactions will often be spontaneous, but ΔG may not be negative (or zero) if ΔS is negative. Endothermic reactions (positive ΔH) can be spontaneous; ΔG can be negative (or zero) if ΔS is positive.
If the entropy change of the system ΔS is positive this may lead to a spontaneous reaction; ΔG will be negative (or zero) if the reaction is also exothermic (negative ΔH). However, if the reaction is endothermic (positive ΔH) then ΔG may not be less than or equal to zero so the reaction will not be spontaneous.
In the following reaction the signs for the energy changes are as follows: ΔH is positive and ΔS is positive. When will the reaction be thermodynamically spontaneous?
CaCO3(s) → CaO(s) + CO2(g)
For a reaction to be thermodynamically spontaneous the change in Gibb's free energy (ΔG) must be equal to or less than zero (there must be an overall gain in entropy in the universe). Since ΔG = ΔH−TΔS (this should be learned), the correct answer is the reaction will become spontaneous at higher temperature since at some point as temperature increases ΔG ≤ 0.
Looking carefully at the Gibb's free energy equation, ΔG = ΔH−TΔS, if ΔH is positive and ΔS is positive then ΔG will be negative when |TΔS| > |ΔH|; this will occur as temperature increases, as |TΔS| becomes greater as temperature becomes greater.
Note: |x| means magnitude of x, that is the numerical value of x without a sign.
Remember: Temperature, T in the expression is given in Kelvin (K) so is always positive.
Incorrect answers (refer to ΔG = ΔH−TΔS)
For the reaction to be become spontaneous at lower temperature, ΔH and ΔS would both need to be negative; then ΔG will be negative when |TΔS| < |ΔH|; this will occur as temperature decreases, as |TΔS| becomes smaller as temperature becomes smaller.
For the reaction to always be spontaneous (at any temperature), ΔH would need to be negative and ΔS would need to be positive; then ΔG will always be negative.
For the reaction to never be spontaneous (at any temperature), ΔH would need to be positive and ΔS would need to be negative; then ΔG will always be positive.
Which units are entropy changes (ΔS) and enthalpy changes (ΔH) usually quoted in?
Calculator question: The hydrogenation of propyne is shown below:
C3H4(g) + 2H2(g) → C3H8(g)
The energy changes for the reaction are as follows:
ΔHo = −287 kJ mol–1
ΔSo = −240 J K–1 mol–1
What is the standard free energy change (ΔGo) at 298K (in kJ mol–1) to three sig figs for the reaction as written above, and is the reaction spontaneous at this temperature?
The standard free energy change (ΔGo) can be calculated by using ΔGo = ΔHo–TΔSo.
Temperature must be in K (as given in the question).
Units for enthalpy include kilojoules and units for entropy include joules. So it is best to convert entropy into kilojoules by dividing by 1000; −240 J K–1 mol–1 becomes −0.240 kJ K–1 mol–1.
Therefore ΔGo = −287−(298×−0.240)
= −215.48 = –215 kJ mol–1 to three sig figs
The standard free energy value is negative, so the reaction is spontaneous. Reactions are spontaneous (meaning 'allowed'; that they will take place if given sufficient activation energy) if the ΔG value is less than or equal to zero.
Thus the correct answer is –215; yes, it is spontaneous.
Incorrect answers
+71200 (+71233) is obtained if entropy value (−240) is not converted into kilojoules.
Calculator question: The reduction of iron oxide is shown below:
Fe2O3(s) + 3H2(g) → 2Fe(s) + 3H2O(l)
The energy changes for the reaction are as follows:
ΔHo = +96.0 kJ mol–1
ΔSo = +138 J K–1 mol–1
What is the standard free energy change (ΔGo) at 20°C (in kJ mol–1) to three sig figs for the reaction as written above?
The standard free energy change (ΔGo) can be calculated by using ΔGo = ΔHo–TΔSo.
Temperature must be in K (Add 273 to °C to get temperature in K); so 20+273= 293K.
Units for enthalpy include kilojoules and units for entropy include joules. So it is best to convert entropy into kilojoules by dividing by 1000; +138 J K–1 mol–1 becomes +0.138 kJ K–1 mol–1.
Therefore ΔGo = +96−(293×+0.138) = 96−40.434
= +55.566 = +55.6 kJ mol–1 to three sig figs
Thus the correct answer is +55.6
(The standard free energy value is positive, so the reaction is not spontaneous. Reactions are spontaneous (meaning 'allowed'; that they will take place if given sufficient activation energy) if the ΔG value is less than or equal to zero.)
Incorrect answers
−40300 (−40338) is obtained if entropy value (+138) is not converted into kilojoules.
+93.2 (+93.24) is obtained if the temperature is not converted into Kelvin; 20 is used as a value instead of 293.
−2660 (−2664) is obtained if entropy value (+138) is not converted into kilojoules and the temperature is not converted into Kelvin; 20 is used as a value instead of 293.
Calculator question: The reduction of iron oxide is shown below:
Fe2O3(s) + 3H2(g) → 2Fe(s) + 3H2O(l)
The energy changes for the reaction are as follows:
ΔHo = +96.0 kJ mol–1
ΔSo = +138 J K–1 mol–1
The reaction is not spontaneous at 298K (25°C) but does becomes spontaneous at higher temperature. To three sig figs, at what temperature (in Kelvin, K) will the reaction become spontaneous?
The standard free energy change (ΔGo) can be calculated by using ΔGo = ΔHo–TΔSo.
Reactions are spontaneous (meaning 'allowed'; that they will take place if given sufficient activation energy) if the ΔG value is less than or equal to zero. So to find the point at which the reaction becomes spontaneous we must calculate the temperature at which ΔGo = 0.
Units for enthalpy include kilojoules and units for entropy include joules. So it is best to convert entropy into kilojoules by dividing by 1000; +138 J K–1 mol–1 becomes +0.138 kJ K–1 mol–1.
Therefore ΔGo = 0 = +96−(T×+0.138)
Rearranging:
−(T×+0.138) = −96
(T×+0.138) = 96
T = 96/0.138
= 695.652174 = 696K to three sig figs
Thus the correct answer is 696
Incorrect answers
0.696 is obtained if entropy value (+138) is not converted into kilojoules.
54.9 (54.876) is the ΔGo value (in kJ mol–1) obtained if the values given in the question are plugged into ΔGo = ΔHo–TΔSo (at 298K).
13.2 (13.248) is obtained if T = 96×0.138 instead of 96÷0.138 (rearranging error).
Paper 1
Core (SL&HL): Energetics core (SL and HL) paper 1 questions
AHL (HL only): Energetics AHL (HL only) paper 1 questions
Paper 2
Core (SL&HL): Energetics core (SL & HL) paper 2 questions
AHL (HL only): Energetics AHL (HL only) paper 2 questions
How much of Entropy and spontaneity have you understood?

















 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn