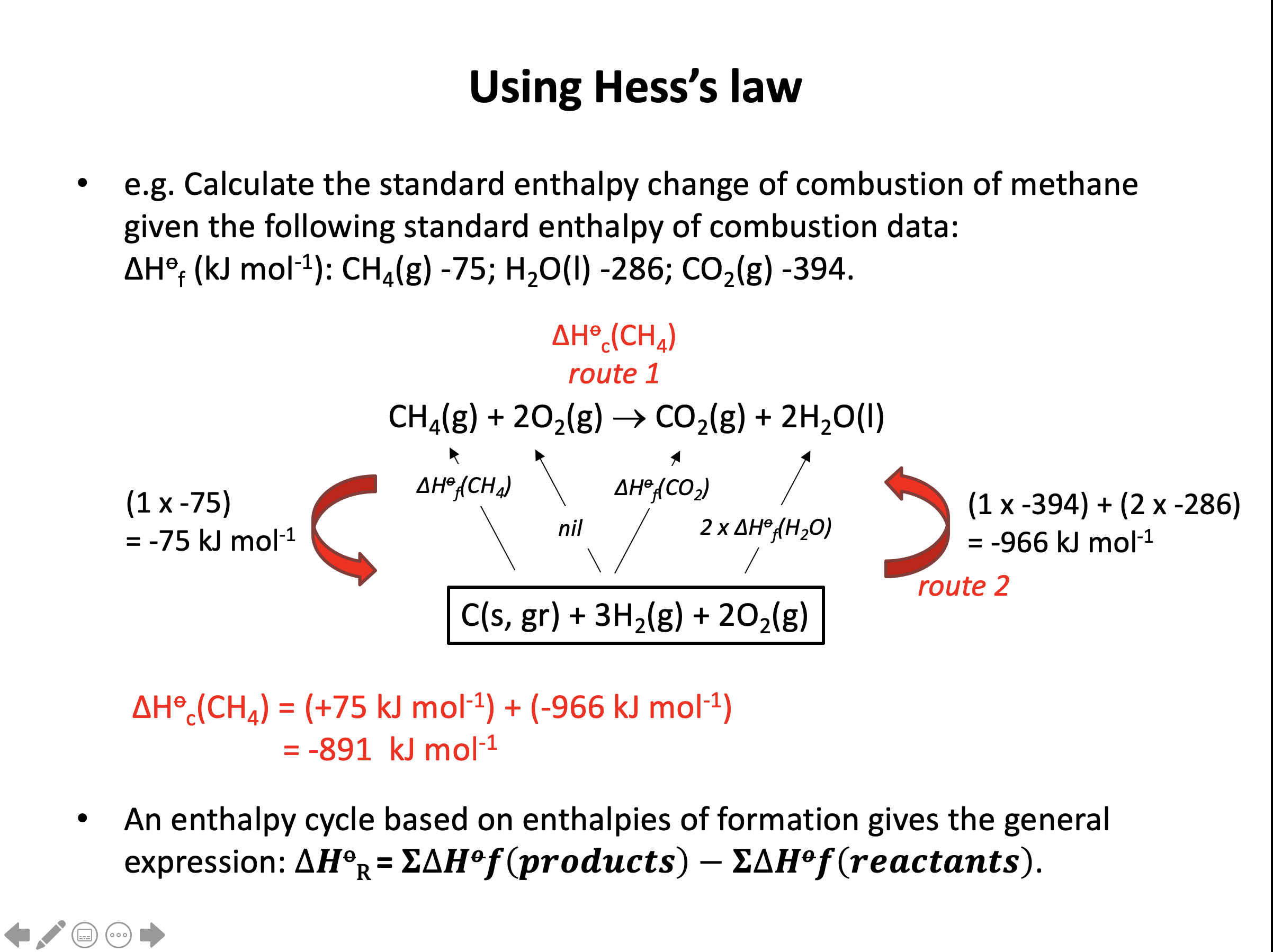
 It is not always possible to measure the enthalpy change of a reaction directly. Energy cycles offer an indirect route, using the known enthalpy changes of other reactions. Energy cannot be created or destroyed (1st law of thermodynamics), so the sum of all the individual steps in a complete energy cycle must equal zero. This is Hess’s law.
It is not always possible to measure the enthalpy change of a reaction directly. Energy cycles offer an indirect route, using the known enthalpy changes of other reactions. Energy cannot be created or destroyed (1st law of thermodynamics), so the sum of all the individual steps in a complete energy cycle must equal zero. This is Hess’s law.
You must be confident with the definitions of different enthalpy changes as these determine how the data in a Hess cycle needs to be manipulated, so use the flash cards to learn the vocabulary thoroughly. Hess cycles are not difficult but can quickly become confusing. Refer to revision cards 2, 4 and 5 to help you organise your thoughts and working.
Ensure you are confident using the terms below and learn the asterisked* definitions
Hess law*, standard enthalpy change of combustion (ΔHoc)*, standard enthalpy change of neutralisation (ΔHon)*, standard enthalpy change of formation (ΔHof)*
Using the energy cycle below which is the correct expression for the calculation of ΔHZ?
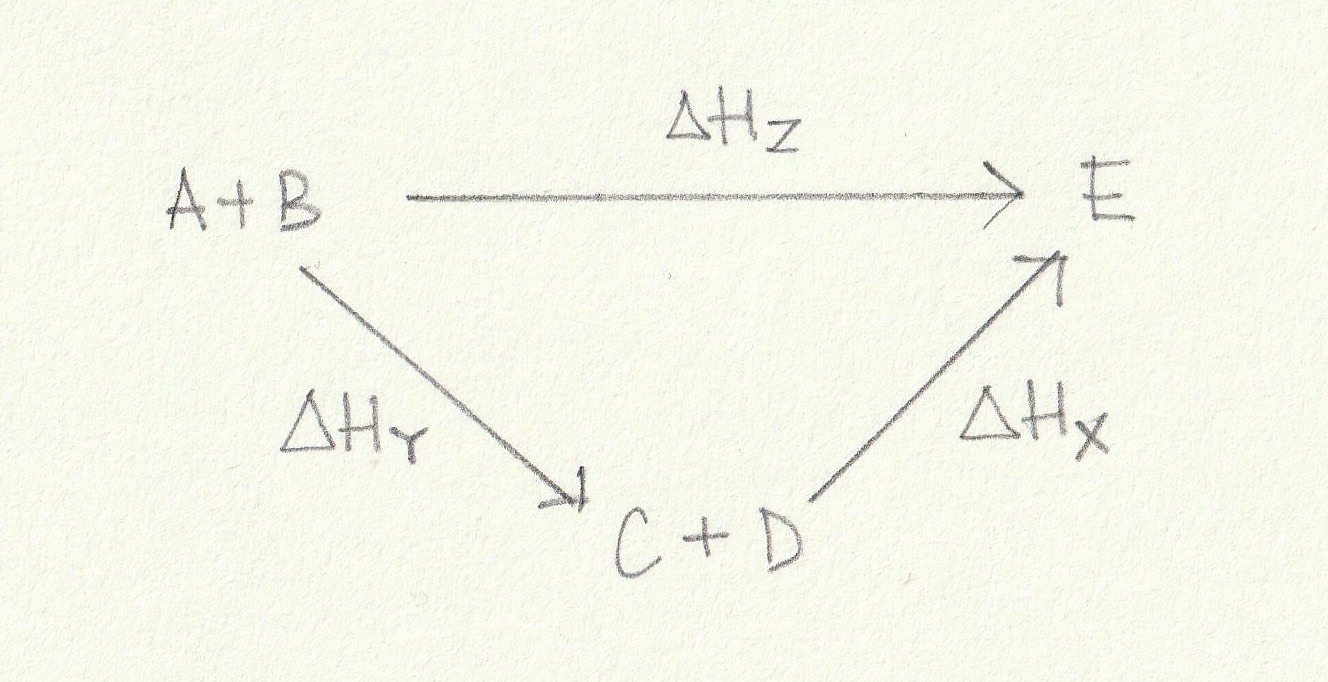
ΔHZ is the enthalpy change from A+B→E. An alternative route is to go from A+B→C+D and then on from C+D→E. This alternative route 'goes with' the arrows of the enthalpy changes shown so the signs (indicating the exothermic or endothermic nature) of the enthalpy changes will remain unchanged.
Thus the correct answer is ΔHZ = ΔHY + ΔHX
Using the energy cycle below which is the correct expression for the calculation of ΔHA?
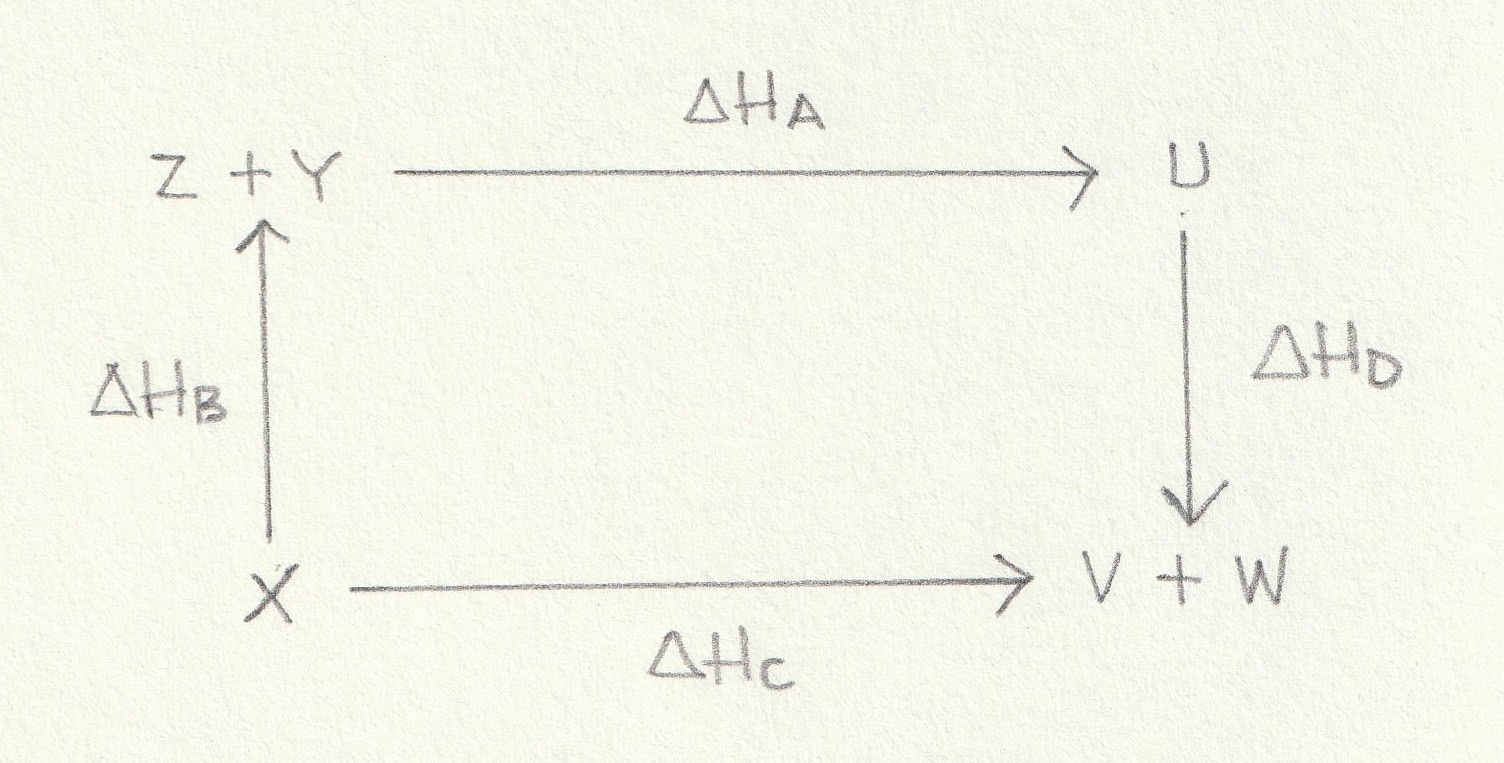
ΔHA is the enthalpy change from Z+Y→U. An alternative route is to go from Z+Y→X (against the arrow) and then on from X→V+W (with the arrow) and then on from V+W→U (against the arrow). This alternative route goes against the arrows of the enthalpy changes ΔHB and ΔHD so the signs (indicating the exothermic or endothermic nature) of the enthalpy changes will need to be inverted by applying a negaitve sign. However, this alternative route goes with the arrow of the enthalpy changes ΔHC so the sign (indicating the exothermic or endothermic nature) of this enthalpy change will remain unchanged.
Thus the correct answer is ΔHZ = − ΔHB + ΔHC − ΔHD
Using the standard enthalpies of combustion from the data book (also given below), what is ΔH for the following reaction (in kJ mol−1)?
2C(s) + 3H2(g) → C2H6(g)
ΔHc°(C(s)) = −394 kJ mol−1
ΔHc°(H2(g)) = −286 kJ mol−1
ΔHc°(C2H6(g)) = −1561 kJ mol−1
We are given ΔH combustion data so we construct the energy cycle by linking the reactants and products through the combustion products:

The enthalpy change for the reaction given (Y) can then be found: The alternative route going via the combustion products is therefore Y = X−Z (−Z because we are going against the arrow so the sign must be inverted).
Change X is the combustion of two moles of C(s) and three moles of H2(g) and change Z is the combustion of one mole of C2H6(g) so the calculation is as follows:
X = (2×−394)+(3×−286) = −1646
Z = −1561
Y = X−Z = −1646−(−1561) = −85 kJ mol−1
The correct answer is therefore −85
Incorrect answers
+85 is obtained if the signs of changes X and Z are inverted.
+881 is obtained if the the mole quantities are ignored and one mole of each of C and H2 are used to obtain change X.
−3207 is obtained if both changes are added together: Y = X + Z
Using the standard enthalpies of combustion from the data book (also given below), what is ΔH for the following reaction (in kJ mol−1)?
2C(s) + O2(g) → 2CO(g)
ΔHc°(C(s)) = −394 kJ mol−1
ΔHc°(CO(g)) = −283 kJ mol−1
We are given ΔH combustion data so we construct the energy cycle by linking the reactants and products through the combustion products:

The enthalpy change for the reaction given (K) can then be found: The alternative route going via the combustion products is therefore K = J−L (−L because we are going against the arrow so the sign must be inverted).
Change J is the combustion of two moles of C(s) (we can ignore the O2(g) since oxygen doesn't combust itself) and change L is the combustion of two moles of CO(g) so the calculation is as follows:
J = 2×−394 = −788
L = 2×−283 = −566
K = J−L = −788−(−566) = −222 kJ mol−1
The correct answer is therefore −222
Incorrect answers
+222 is obtained if the signs of changes J and L are inverted.
−111 is obtained if the the mole quantities are ignored and one mole of each of C and CO are used.
+111 is obtained if the the mole quantities are ignored and one mole of each of C and CO are used and the the signs of changes J and L are inverted.
Using the standard enthalpies of formation from the data book (also given below), what is ΔH for the following reaction (to 4 sig figs; in kJ mol−1)?
C5H12(l) + 8O2(g) → 5CO2(g) + 6H2O(l)
ΔHf°(C5H12(l)) = −173.0 kJ mol−1
ΔHf°(CO2(g)) = −393.5 kJ mol−1
ΔHf°(H2O(l)) = −285.8 kJ mol−1
We are given ΔH formation data so we construct the energy cycle by linking the reactants and products through the elements:

The enthalpy change for the reaction given (A) can then be found: The alternative route going via the elements is therefore A = −B+C (−B because we are going against the arrow so the sign must be inverted).
Change B is the formation of one mole of C5H12(l) (the ΔH formation of any element (O2(g) here) is by definition zero) and change C is the formation of five moles of CO2(g) and six moles of H2O(l) so the calculation is as follows:
B = −173
C = (5×−393.5)+(6×−285.8) = −3682.3
A = −B+C = −(−173)+(−3682.3) = −3509.3 kJ mol−1
The correct answer is therefore −3509 (4 sig figs)
Incorrect answers
+3509 is obtained if the signs of changes B and C are inverted.
−506.3 is obtained if the the mole quantities are ignored and one mole of each of CO2 and H2O are used.
−3855 is obtained if both changes are added together: A = B + C
Using the standard enthalpies of formation from the data book (also given below), what is ΔH for the following reaction (to 4 sig figs; in kJ mol−1)?
C3H6(g) + 4½O2(g) → 3CO2(g) + 3H2O(l)
ΔHf°(C3H6(g)) = +20.0 kJ mol−1
ΔHf°(CO2(g)) = −393.5 kJ mol−1
ΔHf°(H2O(l)) = −285.8 kJ mol−1
We are given ΔH formation data so we construct the energy cycle by linking the reactants and products through the elements:

The enthalpy change for the reaction given (E) can then be found: The alternative route going via the elements is therefore E = −F+G (−F because we are going against the arrow so the sign must be inverted).
Change F is the formation of one mole of C3H6(g) (the ΔH formation of any element (O2(g) here) is by definition zero) and change G is the formation of three moles of CO2(g) and three moles of H2O(l) so the calculation is as follows:
F = +20.0
G = (3×−393.5)+(3×−285.8) = −2037.9
E = −F+G = −(+20.0)+(−2037.9) = −2057.9 kJ mol−1
The correct answer is therefore −2058 (4 sig figs)
Incorrect answers
+2058 is obtained if the signs of changes F and G are inverted.
−699.3 is obtained if the the mole quantities are ignored and one mole of each of CO2 and H2O are used.
−2018 is obtained if both changes are added together: E = F + G
Using the ΔH values for the reactions given below (i, ii, iii) , what is ΔH for the following reaction; the formation of carbon disulfide (in kJ mol−1)?
C(s) + ¼S8(s) → CS2(l)
(i) S8(s) + 8O2(g) → 8SO2(g) ΔH° = −2376 kJ mol−1
(ii) CS2(l) + 3O2(g) → CO2(g) + 2SO2(g) ΔH° = −1072 kJ mol−1
(iii) C(s) + O2(g) → CO2(g) ΔH° = −394 kJ mol−1
We are given ΔH data that shows reactions with oxygen (probably combustion) so we construct the energy cycle by linking the reactants and products through the combustion products:

The enthalpy change for the reaction given ('A') can then be found: The alternative route going via the combustion products is therefore A = B−C (−C because we are going against the arrow so the sign must be inverted).
Change 'B' is the combustion of one mole of C(s) (reaction iii) and one quarter of a mole of S8(S) (so one quarter of the value of reaction i) and change 'C' is the combustion of one mole of CS2(g) as given in reaction ii. So the calculation is as follows:
B = −394+(¼×−2376) = −988
C = −1072
A = B−C = −988−(−1072) = +84 kJ mol−1
The correct answer is therefore +84
Incorrect answers
−1304 is obtained if A = i − ii is taken to be the answer.
−1698 is obtained if one quarter of the value for reaction i is not taken (the full value of −2376 is used and all other calculations are correct).
−2060 is obtained if the values for B and C are added together (A = B + C)
Paper 1
Core (SL&HL): Energetics core (SL and HL) paper 1 questions
AHL (HL only): Energetics AHL (HL only) paper 1 questions
Paper 2
Core (SL&HL): Energetics core (SL & HL) paper 2 questions
AHL (HL only): Energetics AHL (HL only) paper 2 questions
How much of Hess's Law have you understood?













 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn