IB Questionbank

Loading [MathJax]/jax/element/mml/optable/GeneralPunctuation.js

Updates to Questionbank

User interface language: English | Español

Date	May 2017	Marks available	1	Reference code	17M.2.SL.TZ1.S_7
Level	Standard Level	Paper	Paper 2	Time zone	Time zone 1
Command term	Write down	Question number	S_7	Adapted from	N/A

Question

A particle P moves along a straight line. Its velocity ${v_{\text{P}}}{\text{ m}}\,{{\text{s}}^{ - 1}}$ after $t$ seconds is given by ${v_{\text{P}}} = \sqrt t \sin \left( {\frac{\pi }{2}t} \right)$ , for $0 \leqslant t \leqslant 8$ . The following diagram shows the graph of ${v_{\text{P}}}$ .

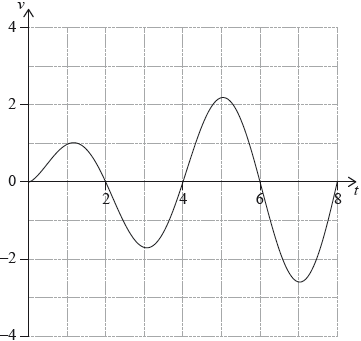
M17/5/MATME/SP2/ENG/TZ1/07

Write down the first value of $t$ at which P changes direction.

[1]

a.i.

Find the total distance travelled by P, for $0 \leqslant t \leqslant 8$ .

[2]

a.ii.

A second particle Q also moves along a straight line. Its velocity, ${v_{\text{Q}}}{\text{ m}}\,{{\text{s}}^{ - 1}}$ after $t$ seconds is given by ${v_{\text{Q}}} = \sqrt t$ for $0 \leqslant t \leqslant 8$ . After $k$ seconds Q has travelled the same total distance as P.

Find $k$ .

[4]

b.

Markscheme

$t = 2$ A1 N1

[1 mark]

a.i.

substitution of limits or function into formula or correct sum (A1)

eg $\,\,\,\,\,$ $\int_0^8 {\left| v \right|{\text{d}}t,{\text{ }}\int {\left| {{v_Q}} \right|{\text{d}}t,{\text{ }}\int_0^2 {v{\text{d}}t - \int_2^4 {v{\text{d}}t + \int_4^6 {v{\text{d}}t - \int_6^8 {v{\text{d}}t} } } } } }$

9.64782

distance $= 9.65{\text{ (metres)}}$ A1 N2

[2 marks]

a.ii.

correct approach (A1)

eg $\,\,\,\,\,$ $s = \int {\sqrt t ,{\text{ }}\int_0^k {\sqrt t } } {\text{d}}t,{\text{ }}\int_0^k {\left| {{v_{\text{Q}}}} \right|{\text{d}}t}$

correct integration (A1)

eg $\,\,\,\,\,$ $\int {\sqrt t = \frac{2}{3}{t^{\frac{3}{2}}} + c,{\text{ }}\left[ {\frac{2}{3}{x^{\frac{3}{2}}}} \right]_0^k,{\text{ }}\frac{2}{3}{k^{\frac{3}{2}}}}$

equating their expression to the distance travelled by their P (M1)

eg $\,\,\,\,\,$ $\frac{2}{3}{k^{\frac{3}{2}}} = 9.65,{\text{ }}\int_0^k {\sqrt t {\text{d}}t = 9.65}$

5.93855

5.94 (seconds) A1 N3

[4 marks]

b.

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

b.

Syllabus sections

Topic 5—Calculus » AHL 5.13—Kinematic problems

Show 63 related questions

22M.2.AHL.TZ2.6a.i:
Find the initial speed of the ball.
22M.2.AHL.TZ2.6a.ii:
Find the angle of elevation of the ball as it is launched.
22M.1.AHL.TZ2.17b.i:
Find the time taken for the snail to reach the point $(10, 2)$ .
19M.2.SL.TZ2.S_8e.i:
Given that particles A and B start at the same point, find the displacement function ${s_{\text{B}}}$ for particle B.
19M.2.SL.TZ2.S_8c:
Find the value of $t$ when particle A first changes direction.
18M.2.SL.TZ2.S_9d:
Find the acceleration of P when it changes direction.
19M.2.SL.TZ2.S_8d:
Find the total distance travelled by particle A in the first 3 seconds.
21M.2.AHL.TZ2.6b:
Find the magnitude of the particle’s acceleration at $6$ seconds.
22M.1.AHL.TZ2.16b:
Show that the acceleration vector of $P$ is never parallel to the position vector of $P$ .
22M.1.AHL.TZ2.17b.ii:
Hence show that the snail reaches the point $(10, 2)$ before the water does.
21N.1.AHL.TZ0.8b:
Juri starts at a height of $60$ metres and finishes at $F$ , where $x = f$ .

Sketch a possible diagram of the hill on the following pair of coordinate axes.
22M.1.AHL.TZ2.16a:
Find the velocity vector of $P$ .
22M.1.AHL.TZ2.17a:
When $W$ has an $x$ -coordinate equal to $1$ , find the horizontal component of the velocity of $W$ .
18M.2.AHL.TZ2.H_7a:
Determine the first time t₁ at which P has zero velocity.
17M.2.AHL.TZ1.H_11b:
Calculate the vertical distance Xavier travelled in the first 10 seconds.
19M.1.SL.TZ1.S_7b:
Find the total distance travelled in the first 5 seconds.
18M.2.SL.TZ2.S_9e:
Find the total distance travelled by P.
18M.2.SL.TZ2.S_9a:
Find the initial velocity of P.
17M.2.AHL.TZ1.H_11c:
Determine the value of $h$ .
17N.2.SL.TZ0.S_9a:
Write down the values of $t$ when $a = 0$ .
18M.2.SL.TZ2.S_9b:
Find the maximum speed of P.
18M.2.AHL.TZ2.H_7b.ii:
Find the value of the acceleration of P at time t₁.
17M.2.SL.TZ1.S_7a.ii:
Find the total distance travelled by P, for $0 \leqslant t \leqslant 8$ .
17M.2.SL.TZ2.S_7:
Note: In this question, distance is in metres and time is in seconds.

A particle moves along a horizontal line starting at a fixed point A. The velocity $v$ of the particle, at time $t$ , is given by $v(t) = \frac{{2{t^2} - 4t}}{{{t^2} - 2t + 2}}$ , for $0 \leqslant t \leqslant 5$ . The following diagram shows the graph of $v$

There are $t$ -intercepts at $(0,{\text{ }}0)$ and $(2,{\text{ }}0)$ .

Find the maximum distance of the particle from A during the time $0 \leqslant t \leqslant 5$ and justify your answer.
21M.2.AHL.TZ1.6b:
Show that the magnitude of the velocity of the ice-skater at time $t$ is given by

$a e^{b t} \sqrt{(1 + b^{2})}$ .
16N.2.SL.TZ0.S_9b:
Find the value of $p$ .
19M.2.SL.TZ2.S_8b:
Find the value of $t$ when particle A first reaches point P.
18N.2.SL.TZ0.S_4a:
Find when the particle is at rest.
17N.2.SL.TZ0.S_9b:
Hence or otherwise, find all possible values of $t$ for which the velocity of P is decreasing.
17M.2.SL.TZ1.S_7b:
A second particle Q also moves along a straight line. Its velocity, ${v_{\text{Q}}}{\text{ m}}\,{{\text{s}}^{ - 1}}$ after $t$ seconds is given by ${v_{\text{Q}}} = \sqrt t$ for $0 \leqslant t \leqslant 8$ . After $k$ seconds Q has travelled the same total distance as P.

Find $k$ .
19M.2.SL.TZ2.S_8a:
Find the initial displacement of particle A from point P.
21M.2.AHL.TZ2.6c:
Find the greatest speed of $P$ in the interval $0 \leq t \leq 6$ .
18N.2.SL.TZ0.S_4c:
Find the total distance travelled by the particle.
17N.2.SL.TZ0.S_9c:
Find an expression for the velocity of P at time $t$ .
18M.2.SL.TZ2.S_9c:
Write down the number of times that the acceleration of P is 0 m s⁻² .
16N.2.SL.TZ0.S_9c:
(i) Find the value of $q$ .

(ii) Hence, find the speed of P when $t = q$ .
19M.2.AHL.TZ2.H_6:
A particle moves along a horizontal line such that at time $t$ seconds, $t$ ≥ 0, its acceleration $a$ is given by $a$ = 2 $t$ − 1. When $t$ = 6 , its displacement $s$ from a fixed origin O is 18.25 m. When $t$ = 15, its displacement from O is 922.75 m. Find an expression for $s$ in terms of $t$ .
EXN.2.AHL.TZ0.7c.iii:
How many complete revolutions has the ball completed from $t = 0$ to the instant at which the string breaks?
17N.2.SL.TZ0.S_9d:
Find the total distance travelled by P when its velocity is increasing.
17M.1.AHL.TZ2.H_4a:
Find ${t_1}$ and ${t_2}$ .
16N.2.SL.TZ0.S_9a:
Find the initial velocity of $P$ .
21M.2.AHL.TZ2.6d:
The particle starts from the origin $O$ . Find an expression for the displacement of $P$ from $O$ at time $t$ seconds.
16N.2.SL.TZ0.S_9d:
(i) Find the total distance travelled by P between $t = 1$ and $t = p$ .

(ii) Hence or otherwise, find the displacement of P from A when $t = p$ .
21M.2.AHL.TZ1.6d:
Find the magnitude of the velocity of the ice-skater when $t = 2$ .
21M.2.AHL.TZ1.6e:
At a point $P$ , the ice-skater is skating parallel to the $y$ -axis for the first time.

Find $OP$ .
21M.2.AHL.TZ1.6c:
Find the value of $a$ and the value of $b$ .
19M.1.SL.TZ1.S_7a:
Find the value of $s\left( 4 \right) - s\left( 2 \right)$ .
17N.1.AHL.TZ0.H_5:
A particle moves in a straight line such that at time $t$ seconds $(t \geqslant 0)$ , its velocity $v$ , in ${\text{m}}{{\text{s}}^{ - 1}}$ , is given by $v = 10t{{\text{e}}^{ - 2t}}$ . Find the exact distance travelled by the particle in the first half-second.
17M.2.AHL.TZ1.H_11a:
Find his velocity when $t = 15$ .
18M.2.AHL.TZ2.H_7b.i:
Find an expression for the acceleration of P at time t.
19M.2.SL.TZ2.S_8e.ii:
Find the other value of $t$ when particles A and B meet.
21M.2.AHL.TZ2.6a:
Find the times when $P$ is at instantaneous rest.
21M.2.AHL.TZ2.6e:
Find the total distance travelled by $P$ in the interval $0 \leq t \leq 4$ .
17M.1.AHL.TZ2.H_4b:
Find the displacement of the particle when $t = {t_1}$
18N.2.SL.TZ0.S_4b:
Find the acceleration of the particle when $t = 2$ .
EXN.2.AHL.TZ0.7b.i:
Find an expression for the velocity of the ball at time $t$ .
21M.2.AHL.TZ1.6a:
Find the velocity vector at time $t$ .
EXN.2.AHL.TZ0.7b.ii:
Hence show that the velocity of the ball is always perpendicular to the position vector of the ball.
EXN.2.AHL.TZ0.7c.i:
Find an expression for the acceleration of the ball at time $t$ .
EXN.2.AHL.TZ0.7a:
Show that the ball is moving in a circle with its centre at $O$ and state the radius of the circle.
EXN.2.AHL.TZ0.7c.ii:
Find the value of $t$ at the instant the string breaks.
21N.1.AHL.TZ0.8a.i:
Identify the $x$ value of the point where $| h' (x) |$ has its maximum value.
21N.1.AHL.TZ0.8a.ii:
Interpret this point in the given context.

Hide related questions

Topic 5—Calculus