DP Physics Questionbank

Option A: Relativity
| Path: |
Description
[N/A]Directly related questions
- 16N.3.SL.TZ0.5c: In the pion reference frame, the Earth moves a distance X before the pion decays. In the Earth...
-
16N.3.SL.TZ0.5b:
A charged pion decays spontaneously in a time of 26 ns as measured in the frame of reference in which it is stationary. The pion moves with a velocity of 0.96c relative to the Earth. Calculate the pion’s lifetime as measured by an observer on the Earth.
- 16N.3.SL.TZ0.6b: Draw, on the diagram, the x′-axis for the reference frame of S.
-
16N.3.SL.TZ0.4b:
In the reference frame of the laboratory the force on X is magnetic.
(i) State the nature of the force acting on X in this reference frame where X is at rest.
(ii) Explain how this force arises.
- 16N.3.SL.TZ0.5a: Define proper length.
-
16N.3.HL.TZ0.8c:
Calculate the energy and the momentum for each photon after the collision.
-
16N.3.HL.TZ0.9b:
Suggest, whether your answer to (a) underestimates or overestimates the correction required to the time signal.
-
16N.3.HL.TZ0.8b:
Determine the speed of the incoming electron.
- 16N.3.SL.TZ0.7c: Draw, for the reference frame of twin A, a spacetime diagram that represents the worldlines for...
-
16N.3.HL.TZ0.9a:
The gravitational field strength at 20 Mm above the surface of the Earth is about 0.6 N kg–1. Estimate the time correction per day needed to the time signals, due to the gravitational redshift.
- 16N.3.SL.TZ0.7d: Suggest how the twin paradox arises and how it is resolved.
- 16N.3.HL.TZ0.8a: Explain, in terms of a conservation law, why two photons need to be created.
-
16N.3.SL.TZ0.6a:
Calculate the angle between the worldline of S and the worldline of the Earth.
- 16N.3.SL.TZ0.6c: An event Z is shown on the diagram. Label the co-ordinates of this event in the reference frame...
- 16N.3.SL.TZ0.4a: Define frame of reference.
- 16N.3.SL.TZ0.7a: Calculate the time taken for the journey in the reference frame of twin A as measured on Earth.
-
16N.3.SL.TZ0.7b:
Determine the time taken for the journey in the reference frame of twin B.
-
17M.3.SL.TZ1.4b:
Calculate the speed v of the train for the ratio .
-
17M.3.SL.TZ1.4d.i:
Draw the time and space axes for observer P’s reference frame on the spacetime diagram.
-
17M.3.SL.TZ1.4d.ii:
Deduce, using the spacetime diagram, which light was turned on first according to observer P.
-
17M.3.SL.TZ1.4e:
A second train is moving at a velocity of –0.70c with respect to the ground.
Calculate the speed of the second train relative to observer P.
-
17M.3.SL.TZ1.4c:
Later the train is travelling at a speed of 0.60c. Observer P measures the length of the train to be 125 m. The train enters a tunnel of length 100 m according to observer Q.
Show that the length of the train according to observer Q is 100 m.
-
17M.3.SL.TZ1.4d.iv:
Demonstrate that the spacetime interval between events B and F is invariant.
-
17M.3.SL.TZ1.3a:
State what is meant by a reference frame.
-
17M.3.SL.TZ1.3b.i:
State and explain whether the force experienced by P is magnetic, electric or both, in reference frame S.
-
17M.3.SL.TZ1.3b.ii:
State and explain whether the force experienced by P is magnetic, electric or both, in the rest frame of P.
-
17M.3.SL.TZ1.4a:
State which of the two time intervals is a proper time.
-
17M.3.SL.TZ1.4d.iii:
Apply a Lorentz transformation to show that the time difference between events B and F according to observer P is 2.5 × 10–7 s.
-
17M.3.SL.TZ2.5c.ii:
State and explain whether the ct coordinate in (c)(i) is less than, equal to or greater than 1.0 m.
-
17M.3.SL.TZ2.3a:
State one prediction of Maxwell’s theory of electromagnetism that is consistent with special relativity.
-
17M.3.HL.TZ2.7a.i:
State what is meant by the event horizon of a black hole.
-
17M.3.SL.TZ2.3b:
A current is established in a long straight wire that is at rest in a laboratory.
A proton is at rest relative to the laboratory and the wire.
Observer X is at rest in the laboratory. Observer Y moves to the right with constant speed relative to the laboratory. Compare and contrast how observer X and observer Y account for any non-gravitational forces on the proton.
-
17M.3.SL.TZ2.5a.i:
Calculate the length of the rocket according to X.
-
17M.3.HL.TZ1.5a:
Calculate the potential difference V.
-
17M.3.SL.TZ2.4:
Muons are unstable particles with a proper lifetime of 2.2 μs. Muons are produced 2.0 km above ground and move downwards at a speed of 0.98c relative to the ground. For this speed = 5.0. Discuss, with suitable calculations, how this experiment provides evidence for time dilation.
-
17M.3.SL.TZ2.5a.ii:
A space shuttle is released from the rocket. The shuttle moves with speed 0.20c to the right according to X. Calculate the velocity of the shuttle relative to the rocket.
-
17M.3.SL.TZ2.5b.i:
the time interval between the lamps turning on.
-
17M.3.SL.TZ2.5b.ii:
which lamp turns on first.
-
17M.3.SL.TZ2.5c.i:
On the diagram label the coordinates x and ct.
-
17M.3.SL.TZ2.5c.iii:
Calculate the value of c 2t 2 – x 2.
-
17M.3.HL.TZ1.6b:
Explain whether the detected frequency would be greater or less than the emitted frequency.
-
17M.3.HL.TZ2.7a.iii:
Suggest why the surface area of the event horizon can never decrease.
-
17M.3.HL.TZ1.6a:
Calculate the expected shift in frequency between the emitted and the detected gamma rays.
-
17M.3.HL.TZ2.6:
A lambda 0 particle at rest decays into a proton p and a pion according to the reaction
0 → p + –
where the rest energy of p = 938 MeV and the rest energy of – = 140 MeV.
The speed of the pion after the decay is 0.579c. For this speed = 1.2265. Calculate the speed of the proton.
-
17M.3.HL.TZ2.7a.ii:
Show that the surface area A of the sphere corresponding to the event horizon is given by
.
-
17M.3.HL.TZ1.5b:
The proton collides with an antiproton moving with the same speed in the opposite direction. As a result both particles are annihilated and two photons of equal energy are produced.
Determine the momentum of one of the photons.
-
17M.3.HL.TZ2.7b:
The diagram shows a box that is falling freely in the gravitational field of a planet.
A photon of frequency f is emitted from the floor of the box and is received at the ceiling. State and explain the frequency of the photon measured at the ceiling.
-
20N.3.SL.TZ0.4b(i):
Deduce the length of the probe as measured by an observer in the spaceship.
- 20N.3.SL.TZ0.3c(i): Identify the nature of the attractive force recorded by an observer stationary with respect to...
-
20N.3.SL.TZ0.5a(ii):
Draw the axis for the reference frame of spaceship A.
- 20N.3.SL.TZ0.3a: Maxwell’s equations led to the constancy of the speed of light. Identify what Maxwell’s equations...
- 20N.3.SL.TZ0.3b: State a postulate that is the same for both special relativity and Galilean relativity.
- 20N.3.SL.TZ0.3c(ii): A second observer moves at the drift velocity of the electron current in the wires. Discuss how...
- 20N.3.SL.TZ0.4a: The Lorentz transformations assume that the speed of light is constant. Outline what the Galilean...
-
20N.3.SL.TZ0.4b(ii):
Explain which of the lengths is the proper length.
-
20N.3.SL.TZ0.5a(i):
Calculate in terms of the velocity of spaceship A relative to observer O.
-
20N.3.SL.TZ0.5b(ii):
Determine the time, according to spaceship A, when light from event E was observed on spaceship A.
-
20N.1.SL.TZ0.4c:
Calculate the speed of the probe in terms of , relative to Earth.
-
20N.3.SL.TZ0.5b(i):
Plot the event E on the spacetime diagram and label it E.
-
20N.3.HL.TZ0.6b:
Calculate the total energy of the deuterium particle in .
-
20N.3.HL.TZ0.7b(ii):
Explain the cause of the frequency shift for the gamma rays in your answer in (a) if the tower and detector were accelerating towards the gamma rays in free space.
- 20N.3.HL.TZ0.6c: In relativistic reactions the mass of the products may be less than the mass of the reactants....
-
20N.3.HL.TZ0.7b(i):
Explain the cause of the frequency shift for the gamma rays in your answer in (a) in the Earth’s gravitational field.
-
20N.3.HL.TZ0.7a:
Calculate the fractional change in frequency of the gamma rays at the detector.
- 20N.3.HL.TZ0.6a: Define rest mass.
-
20N.3.SL.TZ0.4c:
Calculate the speed of the probe in terms of , relative to Earth.
-
17N.3.HL.TZ0.8a:
Outline why the clock near the black hole runs slowly compared to a clock close to the distant observer.
-
17N.3.HL.TZ0.8b:
Calculate the number of ticks detected in 10 ks by the distant observer.
-
17N.3.HL.TZ0.7a:
Determine the rest mass of the particle.
-
17N.3.HL.TZ0.7b:
Determine, using your answer to (a), the initial speed of the particle.
-
17N.3.SL.TZ0.5c:
Identify the terms in the formula.
u′ =
- 17N.3.SL.TZ0.4: Outline the conclusion from Maxwell’s work on electromagnetism that led to one of the postulates...
- 17N.3.SL.TZ0.5a: Define frame of reference.
- 17N.3.SL.TZ0.5b: Calculate, according to the observer on Earth, the time taken for A and B to meet.
-
17N.3.SL.TZ0.5d:
Determine, according to an observer in A, the velocity of B.
-
17N.3.SL.TZ0.5e.i:
Determine, according to an observer in A, the time taken for B to meet A.
- 17N.3.SL.TZ0.5e.ii: Deduce, without further calculation, how the time taken for A to meet B, according to an observer...
- 17N.3.SL.TZ0.6b: Draw a spacetime diagram for this situation according to an observer at rest relative to the tunnel.
- 17N.3.SL.TZ0.6c: Calculate the velocity of the train, according to an observer at rest relative to the tunnel, at...
-
17N.3.SL.TZ0.6d:
For an observer on the train, it is the tunnel that is moving and therefore will appear length contracted. This seems to contradict the observation made by the observer at rest to the tunnel, creating a paradox. Explain how this paradox is resolved. You may refer to your spacetime diagram in (b).
-
18M.3.HL.TZ1.6b:
State the rest mass of the pion with an appropriate unit.
-
18M.3.HL.TZ1.7c:
Observer A now sends a beam of light initially parallel to the surface of the planet.
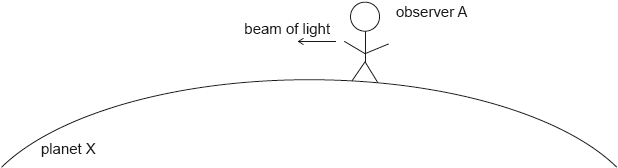
Explain why the path of the light is curved.
-
18M.3.HL.TZ1.6a.ii:
show that the energy of the pion is about 140 MeV.
-
18M.3.HL.TZ1.7a:
Calculate the shift in frequency observed by A in terms of Δf.
-
18M.3.HL.TZ1.7b:
Calculate the gravitational field strength on the surface of planet X.
The following data is given:
Δf = 170 Hz.
The distance between observer A and B is 10 km.
-
18M.3.SL.TZ1.4a.i:
Calculate, according to Galilean relativity, the time taken for a muon to travel to the ground.
-
18M.3.SL.TZ1.4b.ii:
Discuss how your result in (b)(i) and the outcome of the muon decay experiment support the theory of special relativity.
-
18M.3.SL.TZ1.5b:
Deduce, showing your working on the spacetime diagram, the value of ct according to the Earth observer at which the rocket B emitted its flash of light.
-
18M.3.SL.TZ1.5a:
Draw on the spacetime diagram the worldline of B according to the Earth observer and label it B.
-
18M.3.SL.TZ1.3a:
State whether the field around the wire according to observer X is electric, magnetic or a combination of both.
-
18M.3.SL.TZ1.5c:
Explain whether or not the arrival times of the two flashes in the Earth frame are simultaneous events in the frame of rocket A.
-
18M.3.SL.TZ1.5d:
Calculate the velocity of rocket B relative to rocket A.
-
18M.3.SL.TZ1.3b.ii:
Deduce whether the overall field around the wire is electric, magnetic or a combination of both according to observer Y.
-
18M.3.SL.TZ1.4b.i:
Calculate, according to the theory of special relativity, the time taken for a muon to reach the ground in the reference frame of the muon.
-
18M.3.SL.TZ1.3b.i:
Discuss the change in d according to observer Y.
-
18M.3.SL.TZ1.4a.ii:
Deduce why only a small fraction of the total number of muons created is expected to be detected at ground level according to Galilean relativity.
-
18M.3.SL.TZ2.4a:
Calculate the velocity of the spaceship relative to the Earth.
-
18M.3.HL.TZ2.6a:
Calculate the gamma (γ) factor for one of the protons.
-
18M.3.HL.TZ2.6b.i:
Determine, in terms of MeV c–1, the momentum of the pion.
-
18M.3.HL.TZ2.6b.ii:
The diagram shows the paths of the incident protons together with the proton and neutron created in the interaction. On the diagram, draw the path of the pion.
-
18M.3.HL.TZ2.7a.i:
Outline what is meant by the event horizon of a black hole.
-
18M.3.HL.TZ2.7a.ii:
Calculate the distance of the event horizon of the black hole from its centre.
Mass of Sun = 2 × 1030 kg
-
18M.3.HL.TZ2.7b:
Star S-2 is in an elliptical orbit around a black hole. The distance of S-2 from the centre of the black hole varies between a few light-hours and several light-days. A periodic event on S-2 occurs every 5.0 s.
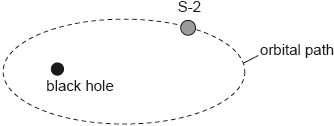
Discuss how the time for the periodic event as measured by an observer on the Earth changes with the orbital position of S-2.
-
18M.3.SL.TZ2.3a.i:
Calculate, for the reference frame of rocket A, the speed of rocket B according to the Galilean transformation.
-
18M.3.SL.TZ2.3a.ii:
Calculate, for the reference frame of rocket A, the speed of rocket B according to the Lorentz transformation.
-
18M.3.SL.TZ2.3b:
Outline, with reference to special relativity, which of your calculations in (a) is more likely to be valid.
-
18M.3.SL.TZ2.4b:
The spaceship passes the space station 90 minutes later as measured by the spaceship clock. Determine, for the reference frame of the Earth, the distance between the Earth and the space station.
-
18M.3.SL.TZ2.4c:
As the spaceship passes the space station, the space station sends a radio signal back to the Earth. The reception of this signal at the Earth is event A. Determine the time on the Earth clock when event A occurs.
-
18M.3.SL.TZ2.4d.i:
Construct event A and event B on the spacetime diagram.
-
18M.3.SL.TZ2.4d.ii:
Estimate, using the spacetime diagram, the time at which event B occurs for the spaceship.
-
18M.3.SL.TZ2.5b.i:
calculate the spacetime interval.
-
18M.3.SL.TZ2.5a:
Explain what is meant by the statement that the spacetime interval is an invariant quantity.
-
18M.3.SL.TZ2.5b.ii:
determine the time between them according to observer B.
-
18M.3.SL.TZ2.5c:
Outline why the observed times are different for A and B.
-
18N.3.SL.TZ0.5a.ii:
ct′ = –1.1 m.
-
18N.3.SL.TZ0.4b.ii:
Determine the time it takes the probe to reach the front of the rocket according to an observer at rest on the ground.
- 18N.3.SL.TZ0.5b.i: Label, on the diagram, the space coordinate of event E in the S′ frame. Label this event with the...
- 18N.3.HL.TZ0.6b.i: Explain the origin of each equation.
-
18N.3.SL.TZ0.5a.i:
x′ = 1.5 m.
-
18N.3.SL.TZ0.3b.i:
explain why the time coordinate of E in frame S is .
- 18N.3.HL.TZ0.7a.i: State what is meant by the event horizon of a black hole.
-
18N.3.SL.TZ0.4b.i:
Determine the time it takes the probe to reach the front of the rocket according to an observer at rest in the rocket.
-
18N.3.SL.TZ0.3b.ii:
hence show that the space coordinate of E in frame S is .
- 18N.3.SL.TZ0.5c.i: Using the spacetime diagram, outline without calculation, why observers in frame S′ measure the...
- 18N.3.SL.TZ0.3a: State what is meant by a reference frame.
-
18N.3.SL.TZ0.5b.ii:
Label, on the diagram, the event that has coordinates x′ = 1.0 m and ct′ = 0. Label this event with the letter Q.
- 18N.3.SL.TZ0.5c.ii: Using the spacetime diagram, estimate, in m, the length of this rod in the S′ frame.
-
18N.3.SL.TZ0.4a:
Calculate the speed of the probe relative to the ground.
-
18N.3.HL.TZ0.7a.ii:
The mass of the black hole is 4.0 × 1036 kg. Calculate the Schwarzschild radius of the black hole.
-
18N.3.HL.TZ0.6a:
Show that the momentum of the electron is 1.41 MeV c–1.
- 18N.3.HL.TZ0.6b.ii: Calculate, in MeV c–1, p1 and p2.
-
18N.3.HL.TZ0.7b:
The probe is stationary above the event horizon of the black hole in (a). The probe sends a radio pulse every 1.0 seconds (as measured by clocks on the probe). The spacecraft receives the pulses every 2.0 seconds (as measured by clocks on the spacecraft). Determine the distance of the probe from the centre of the black hole.
- 19M.3.SL.TZ2.5b: Explain why there is no magnetic force on each proton in its own rest frame.
- 19M.3.SL.TZ2.5c: Explain why there must be a resultant repulsive force on the protons in all reference frames.
- 19M.3.SL.TZ2.4ai: Define an inertial reference frame.
- 19M.3.SL.TZ2.5a: Outline why there is an attractive magnetic force on each proton in the laboratory frame.
- 19M.3.SL.TZ2.4aii: As the spaceship passes the Earth it emits a flash of light that travels in the same direction as...
- 19M.3.SL.TZ2.6bii: In the reference frame of the train a ball travels with speed 0.50c from the back to the front of...
-
19M.3.SL.TZ2.4b:
Use your answer to (a)(ii) to describe the paradigm shift that Einstein’s theory of special relativity produced.
- 19M.3.SL.TZ2.6bi: In the reference frame of the train a ball travels with speed 0.50c from the back to the front of...
- 19M.3.SL.TZ2.6a: Define proper length.
- 19M.3.HL.TZ2.8bi: Determine the momentum of the proton.
- 19M.3.HL.TZ2.8a: Define total energy.
-
19M.3.HL.TZ2.8bii:
Determine the speed of the proton.
- 19M.3.SL.TZ2.7ci: Determine, according to an observer on the spaceship as the spaceship passes the planet, the time...
-
19M.3.SL.TZ2.7b:
Label, with the letter E, the event of the spaceship going past the planet.
- 19M.3.SL.TZ2.7cii: Determine, according to an observer on the spaceship as the spaceship passes the planet, the time...
- 19M.3.SL.TZ2.7d: On passing the planet a probe containing the spaceship’s clock and an astronaut is sent back to...
-
19M.3.HL.TZ2.8biii:
Calculate the potential difference V.
-
19M.3.SL.TZ2.7a:
Show, using the spacetime diagram, that the speed of the spaceship relative to the Earth is 0.80c.
-
19M.3.HL.TZ1.6a:
Show that energy is conserved in this decay.
- 19M.3.HL.TZ1.7b.i: State and explain the path of the light ray according to observer X.
-
19M.3.HL.TZ1.6b:
Calculate the speed of the pion.
- 19M.3.HL.TZ1.7a: State the equivalence principle.
- 19M.3.HL.TZ1.7b.ii: State and explain the path of the light ray according to observer Y.
- 19M.3.HL.TZ2.9b: Calculate the frequency change.
- 19M.3.SL.TZ1.3a: State the speed of the flash of light according to an observer on the ground using Galilean...
-
19M.3.SL.TZ1.5d.ii:
Using the spacetime diagram, determine which event occurred first for the spacecraft observer, event 1 or event 2.
-
19M.3.SL.TZ1.5c:
Show that the value of the invariant spacetime interval between events 1 and 2 is 9600 ly2.
- 19M.3.SL.TZ1.5a: Plot, on the axes, the point corresponding to event 2.
- 19M.3.SL.TZ1.3c: State the speed of the flash of light according to an observer on the ground using Einstein’s...
-
19M.3.SL.TZ1.5b:
Suggest whether the rocket launched by the spacecraft might be the cause of the explosion of the asteroid.
- 19M.3.SL.TZ1.5d.i: An observer in the spacecraft measures that events 1 and 2 are a distance of 120 ly apart....
- 19M.3.HL.TZ2.9a: Explain why a change in frequency is expected for the photon detected at the top of the rocket.
-
19M.3.SL.TZ1.4b:
Demonstrate how an observer moving with the same velocity as the muons accounts for the answer to (a)(ii).
- 19M.3.SL.TZ1.3b: State the speed of the flash of light according to an observer on the ground using Maxwell’s...
-
19M.3.SL.TZ1.4a.ii:
Estimate in the Earth frame the fraction of the original muons that will reach the Earth’s surface before decaying according to special relativity.
-
19M.3.SL.TZ1.4a.i:
Estimate in the Earth frame the fraction of the original muons that will reach the Earth’s surface before decaying according to Newtonian mechanics.
-
19M.3.SL.TZ1.5e:
Determine, using the diagram, the speed of the spacecraft relative to the galaxy.
-
19N.3.SL.TZ0.3b(iv):
The velocity of P is 0.30c relative to the laboratory. A second particle Q moves at a velocity of 0.80c relative to the laboratory.
Calculate the speed of Q relative to P.
- 19N.3.SL.TZ0.4b: Outline why LB is the proper length of the bridge.
- 19N.3.SL.TZ0.4c(ii): Demonstrate using the diagram which lamp, according to observer A, was turned on first.
- 19N.3.SL.TZ0.3a: One of the two postulates of special relativity states that the speed of light in a vacuum is the...
-
19N.3.SL.TZ0.4a(i):
Calculate, for observer A, the length LA of the bridge
-
19N.3.SL.TZ0.4a(ii):
Calculate, for observer A, the time taken to cross the bridge.
- 19N.3.SL.TZ0.3b(i): State the nature of the force on the particle P in the reference frame of the laboratory.
-
19N.3.SL.TZ0.3b(iii):
Explain how the force in part (b)(ii) arises.
-
19N.3.SL.TZ0.3b(ii):
Deduce, using your answer to part (a), the nature of the force that acts on the particle P in the rest frame of P.
- 19N.3.SL.TZ0.4c(iii): Demonstrate, using the diagram, which lamp observer A observes to light first.
-
19N.3.SL.TZ0.4c(iv):
Determine the time, according to observer A, between X and Y.
-
19N.3.SL.TZ0.4c(i):
Draw, on the spacetime diagram, the space axis for the reference frame of observer A. Label this axis '.
-
19N.3.HL.TZ0.5a(i):
the total energy.
-
19N.3.HL.TZ0.5a(ii):
the speed.
-
19N.3.HL.TZ0.5b:
Determine the rest mass of X.
-
19N.3.HL.TZ0.6a:
Explain why the frequency of the radio waves detected by the observer is lower than .
-
19N.3.HL.TZ0.6b:
The probe emits 20 short pulses of these radio waves every minute, according to a clock in the probe. Calculate the time between pulses as measured by the observer.
Sub sections and their related questions
Option A: Relativity (Core topics)
- 16N.3.SL.TZ0.4a: Define frame of reference.
-
16N.3.SL.TZ0.4b:
In the reference frame of the laboratory the force on X is magnetic.
(i) State the nature of the force acting on X in this reference frame where X is at rest.
(ii) Explain how this force arises.
- 16N.3.SL.TZ0.5a: Define proper length.
-
16N.3.SL.TZ0.5b:
A charged pion decays spontaneously in a time of 26 ns as measured in the frame of reference in which it is stationary. The pion moves with a velocity of 0.96c relative to the Earth. Calculate the pion’s lifetime as measured by an observer on the Earth.
- 16N.3.SL.TZ0.5c: In the pion reference frame, the Earth moves a distance X before the pion decays. In the Earth...
-
16N.3.SL.TZ0.6a:
Calculate the angle between the worldline of S and the worldline of the Earth.
- 16N.3.SL.TZ0.6b: Draw, on the diagram, the x′-axis for the reference frame of S.
- 16N.3.SL.TZ0.6c: An event Z is shown on the diagram. Label the co-ordinates of this event in the reference frame...
- 16N.3.SL.TZ0.7a: Calculate the time taken for the journey in the reference frame of twin A as measured on Earth.
-
16N.3.SL.TZ0.7b:
Determine the time taken for the journey in the reference frame of twin B.
- 16N.3.SL.TZ0.7c: Draw, for the reference frame of twin A, a spacetime diagram that represents the worldlines for...
- 16N.3.SL.TZ0.7d: Suggest how the twin paradox arises and how it is resolved.
-
17M.3.SL.TZ1.3a:
State what is meant by a reference frame.
-
17M.3.SL.TZ1.3b.i:
State and explain whether the force experienced by P is magnetic, electric or both, in reference frame S.
-
17M.3.SL.TZ1.3b.ii:
State and explain whether the force experienced by P is magnetic, electric or both, in the rest frame of P.
-
17M.3.SL.TZ1.4a:
State which of the two time intervals is a proper time.
-
17M.3.SL.TZ1.4b:
Calculate the speed v of the train for the ratio .
-
17M.3.SL.TZ1.4c:
Later the train is travelling at a speed of 0.60c. Observer P measures the length of the train to be 125 m. The train enters a tunnel of length 100 m according to observer Q.
Show that the length of the train according to observer Q is 100 m.
-
17M.3.SL.TZ1.4d.i:
Draw the time and space axes for observer P’s reference frame on the spacetime diagram.
-
17M.3.SL.TZ1.4d.ii:
Deduce, using the spacetime diagram, which light was turned on first according to observer P.
-
17M.3.SL.TZ1.4d.iii:
Apply a Lorentz transformation to show that the time difference between events B and F according to observer P is 2.5 × 10–7 s.
-
17M.3.SL.TZ1.4d.iv:
Demonstrate that the spacetime interval between events B and F is invariant.
-
17M.3.SL.TZ1.4e:
A second train is moving at a velocity of –0.70c with respect to the ground.
Calculate the speed of the second train relative to observer P.
-
17M.3.SL.TZ2.3a:
State one prediction of Maxwell’s theory of electromagnetism that is consistent with special relativity.
-
17M.3.SL.TZ2.3b:
A current is established in a long straight wire that is at rest in a laboratory.
A proton is at rest relative to the laboratory and the wire.
Observer X is at rest in the laboratory. Observer Y moves to the right with constant speed relative to the laboratory. Compare and contrast how observer X and observer Y account for any non-gravitational forces on the proton.
-
17M.3.SL.TZ2.4:
Muons are unstable particles with a proper lifetime of 2.2 μs. Muons are produced 2.0 km above ground and move downwards at a speed of 0.98c relative to the ground. For this speed = 5.0. Discuss, with suitable calculations, how this experiment provides evidence for time dilation.
-
17M.3.SL.TZ2.5a.i:
Calculate the length of the rocket according to X.
-
17M.3.SL.TZ2.5a.ii:
A space shuttle is released from the rocket. The shuttle moves with speed 0.20c to the right according to X. Calculate the velocity of the shuttle relative to the rocket.
-
17M.3.SL.TZ2.5b.i:
the time interval between the lamps turning on.
-
17M.3.SL.TZ2.5b.ii:
which lamp turns on first.
-
17M.3.SL.TZ2.5c.i:
On the diagram label the coordinates x and ct.
-
17M.3.SL.TZ2.5c.ii:
State and explain whether the ct coordinate in (c)(i) is less than, equal to or greater than 1.0 m.
-
17M.3.SL.TZ2.5c.iii:
Calculate the value of c 2t 2 – x 2.
- 17N.3.SL.TZ0.4: Outline the conclusion from Maxwell’s work on electromagnetism that led to one of the postulates...
- 17N.3.SL.TZ0.5a: Define frame of reference.
- 17N.3.SL.TZ0.5b: Calculate, according to the observer on Earth, the time taken for A and B to meet.
-
17N.3.SL.TZ0.5c:
Identify the terms in the formula.
u′ =
-
17N.3.SL.TZ0.5d:
Determine, according to an observer in A, the velocity of B.
-
17N.3.SL.TZ0.5e.i:
Determine, according to an observer in A, the time taken for B to meet A.
- 17N.3.SL.TZ0.5e.ii: Deduce, without further calculation, how the time taken for A to meet B, according to an observer...
- 17N.3.SL.TZ0.6b: Draw a spacetime diagram for this situation according to an observer at rest relative to the tunnel.
- 17N.3.SL.TZ0.6c: Calculate the velocity of the train, according to an observer at rest relative to the tunnel, at...
-
17N.3.SL.TZ0.6d:
For an observer on the train, it is the tunnel that is moving and therefore will appear length contracted. This seems to contradict the observation made by the observer at rest to the tunnel, creating a paradox. Explain how this paradox is resolved. You may refer to your spacetime diagram in (b).
-
18M.3.SL.TZ1.3a:
State whether the field around the wire according to observer X is electric, magnetic or a combination of both.
-
18M.3.SL.TZ1.3b.i:
Discuss the change in d according to observer Y.
-
18M.3.SL.TZ1.3b.ii:
Deduce whether the overall field around the wire is electric, magnetic or a combination of both according to observer Y.
-
18M.3.SL.TZ1.4a.i:
Calculate, according to Galilean relativity, the time taken for a muon to travel to the ground.
-
18M.3.SL.TZ1.4a.ii:
Deduce why only a small fraction of the total number of muons created is expected to be detected at ground level according to Galilean relativity.
-
18M.3.SL.TZ1.4b.i:
Calculate, according to the theory of special relativity, the time taken for a muon to reach the ground in the reference frame of the muon.
-
18M.3.SL.TZ1.4b.ii:
Discuss how your result in (b)(i) and the outcome of the muon decay experiment support the theory of special relativity.
-
18M.3.SL.TZ1.5a:
Draw on the spacetime diagram the worldline of B according to the Earth observer and label it B.
-
18M.3.SL.TZ1.5b:
Deduce, showing your working on the spacetime diagram, the value of ct according to the Earth observer at which the rocket B emitted its flash of light.
-
18M.3.SL.TZ1.5c:
Explain whether or not the arrival times of the two flashes in the Earth frame are simultaneous events in the frame of rocket A.
-
18M.3.SL.TZ1.5d:
Calculate the velocity of rocket B relative to rocket A.
-
18M.3.SL.TZ2.3a.i:
Calculate, for the reference frame of rocket A, the speed of rocket B according to the Galilean transformation.
-
18M.3.SL.TZ2.3a.ii:
Calculate, for the reference frame of rocket A, the speed of rocket B according to the Lorentz transformation.
-
18M.3.SL.TZ2.3b:
Outline, with reference to special relativity, which of your calculations in (a) is more likely to be valid.
-
18M.3.SL.TZ2.4a:
Calculate the velocity of the spaceship relative to the Earth.
-
18M.3.SL.TZ2.4b:
The spaceship passes the space station 90 minutes later as measured by the spaceship clock. Determine, for the reference frame of the Earth, the distance between the Earth and the space station.
-
18M.3.SL.TZ2.4c:
As the spaceship passes the space station, the space station sends a radio signal back to the Earth. The reception of this signal at the Earth is event A. Determine the time on the Earth clock when event A occurs.
-
18M.3.SL.TZ2.4d.i:
Construct event A and event B on the spacetime diagram.
-
18M.3.SL.TZ2.4d.ii:
Estimate, using the spacetime diagram, the time at which event B occurs for the spaceship.
-
18M.3.SL.TZ2.5a:
Explain what is meant by the statement that the spacetime interval is an invariant quantity.
-
18M.3.SL.TZ2.5b.i:
calculate the spacetime interval.
-
18M.3.SL.TZ2.5b.ii:
determine the time between them according to observer B.
-
18M.3.SL.TZ2.5c:
Outline why the observed times are different for A and B.
- 18N.3.SL.TZ0.3a: State what is meant by a reference frame.
-
18N.3.SL.TZ0.3b.i:
explain why the time coordinate of E in frame S is .
-
18N.3.SL.TZ0.3b.ii:
hence show that the space coordinate of E in frame S is .
-
18N.3.SL.TZ0.4a:
Calculate the speed of the probe relative to the ground.
-
18N.3.SL.TZ0.4b.i:
Determine the time it takes the probe to reach the front of the rocket according to an observer at rest in the rocket.
-
18N.3.SL.TZ0.4b.ii:
Determine the time it takes the probe to reach the front of the rocket according to an observer at rest on the ground.
-
18N.3.SL.TZ0.5a.i:
x′ = 1.5 m.
-
18N.3.SL.TZ0.5a.ii:
ct′ = –1.1 m.
- 18N.3.SL.TZ0.5b.i: Label, on the diagram, the space coordinate of event E in the S′ frame. Label this event with the...
-
18N.3.SL.TZ0.5b.ii:
Label, on the diagram, the event that has coordinates x′ = 1.0 m and ct′ = 0. Label this event with the letter Q.
- 18N.3.SL.TZ0.5c.i: Using the spacetime diagram, outline without calculation, why observers in frame S′ measure the...
- 18N.3.SL.TZ0.5c.ii: Using the spacetime diagram, estimate, in m, the length of this rod in the S′ frame.
- 19M.3.SL.TZ2.4ai: Define an inertial reference frame.
- 19M.3.SL.TZ2.4aii: As the spaceship passes the Earth it emits a flash of light that travels in the same direction as...
-
19M.3.SL.TZ2.4b:
Use your answer to (a)(ii) to describe the paradigm shift that Einstein’s theory of special relativity produced.
- 19M.3.SL.TZ2.5a: Outline why there is an attractive magnetic force on each proton in the laboratory frame.
- 19M.3.SL.TZ2.5b: Explain why there is no magnetic force on each proton in its own rest frame.
- 19M.3.SL.TZ2.5c: Explain why there must be a resultant repulsive force on the protons in all reference frames.
- 19M.3.SL.TZ2.6a: Define proper length.
- 19M.3.SL.TZ2.6bi: In the reference frame of the train a ball travels with speed 0.50c from the back to the front of...
- 19M.3.SL.TZ2.6bii: In the reference frame of the train a ball travels with speed 0.50c from the back to the front of...
-
19M.3.SL.TZ2.7a:
Show, using the spacetime diagram, that the speed of the spaceship relative to the Earth is 0.80c.
-
19M.3.SL.TZ2.7b:
Label, with the letter E, the event of the spaceship going past the planet.
- 19M.3.SL.TZ2.7ci: Determine, according to an observer on the spaceship as the spaceship passes the planet, the time...
- 19M.3.SL.TZ2.7cii: Determine, according to an observer on the spaceship as the spaceship passes the planet, the time...
- 19M.3.SL.TZ2.7d: On passing the planet a probe containing the spaceship’s clock and an astronaut is sent back to...
- 19M.3.SL.TZ1.3a: State the speed of the flash of light according to an observer on the ground using Galilean...
- 19M.3.SL.TZ1.3b: State the speed of the flash of light according to an observer on the ground using Maxwell’s...
- 19M.3.SL.TZ1.3c: State the speed of the flash of light according to an observer on the ground using Einstein’s...
-
19M.3.SL.TZ1.4a.i:
Estimate in the Earth frame the fraction of the original muons that will reach the Earth’s surface before decaying according to Newtonian mechanics.
-
19M.3.SL.TZ1.4a.ii:
Estimate in the Earth frame the fraction of the original muons that will reach the Earth’s surface before decaying according to special relativity.
-
19M.3.SL.TZ1.4b:
Demonstrate how an observer moving with the same velocity as the muons accounts for the answer to (a)(ii).
- 19M.3.SL.TZ1.5a: Plot, on the axes, the point corresponding to event 2.
-
19M.3.SL.TZ1.5b:
Suggest whether the rocket launched by the spacecraft might be the cause of the explosion of the asteroid.
-
19M.3.SL.TZ1.5c:
Show that the value of the invariant spacetime interval between events 1 and 2 is 9600 ly2.
- 19M.3.SL.TZ1.5d.i: An observer in the spacecraft measures that events 1 and 2 are a distance of 120 ly apart....
-
19M.3.SL.TZ1.5d.ii:
Using the spacetime diagram, determine which event occurred first for the spacecraft observer, event 1 or event 2.
-
19M.3.SL.TZ1.5e:
Determine, using the diagram, the speed of the spacecraft relative to the galaxy.
- 19N.3.SL.TZ0.3a: One of the two postulates of special relativity states that the speed of light in a vacuum is the...
- 19N.3.SL.TZ0.3b(i): State the nature of the force on the particle P in the reference frame of the laboratory.
-
19N.3.SL.TZ0.3b(ii):
Deduce, using your answer to part (a), the nature of the force that acts on the particle P in the rest frame of P.
-
19N.3.SL.TZ0.3b(iii):
Explain how the force in part (b)(ii) arises.
-
19N.3.SL.TZ0.3b(iv):
The velocity of P is 0.30c relative to the laboratory. A second particle Q moves at a velocity of 0.80c relative to the laboratory.
Calculate the speed of Q relative to P.
-
19N.3.SL.TZ0.4a(i):
Calculate, for observer A, the length LA of the bridge
-
19N.3.SL.TZ0.4a(ii):
Calculate, for observer A, the time taken to cross the bridge.
- 19N.3.SL.TZ0.4b: Outline why LB is the proper length of the bridge.
-
19N.3.SL.TZ0.4c(i):
Draw, on the spacetime diagram, the space axis for the reference frame of observer A. Label this axis '.
- 19N.3.SL.TZ0.4c(ii): Demonstrate using the diagram which lamp, according to observer A, was turned on first.
- 19N.3.SL.TZ0.4c(iii): Demonstrate, using the diagram, which lamp observer A observes to light first.
-
19N.3.SL.TZ0.4c(iv):
Determine the time, according to observer A, between X and Y.
- 20N.3.SL.TZ0.3a: Maxwell’s equations led to the constancy of the speed of light. Identify what Maxwell’s equations...
- 20N.3.SL.TZ0.3b: State a postulate that is the same for both special relativity and Galilean relativity.
- 20N.3.SL.TZ0.3c(i): Identify the nature of the attractive force recorded by an observer stationary with respect to...
- 20N.3.SL.TZ0.3c(ii): A second observer moves at the drift velocity of the electron current in the wires. Discuss how...
- 20N.3.SL.TZ0.4a: The Lorentz transformations assume that the speed of light is constant. Outline what the Galilean...
-
20N.3.SL.TZ0.4b(i):
Deduce the length of the probe as measured by an observer in the spaceship.
-
20N.3.SL.TZ0.4b(ii):
Explain which of the lengths is the proper length.
-
20N.1.SL.TZ0.4c:
Calculate the speed of the probe in terms of , relative to Earth.
-
20N.3.SL.TZ0.5a(i):
Calculate in terms of the velocity of spaceship A relative to observer O.
-
20N.3.SL.TZ0.5a(ii):
Draw the axis for the reference frame of spaceship A.
-
20N.3.SL.TZ0.5b(i):
Plot the event E on the spacetime diagram and label it E.
-
20N.3.SL.TZ0.5b(ii):
Determine the time, according to spaceship A, when light from event E was observed on spaceship A.
-
20N.3.SL.TZ0.4c:
Calculate the speed of the probe in terms of , relative to Earth.
Option A: Relativity (Additional higher level option topics)
- 16N.3.HL.TZ0.8a: Explain, in terms of a conservation law, why two photons need to be created.
-
16N.3.HL.TZ0.8b:
Determine the speed of the incoming electron.
-
16N.3.HL.TZ0.8c:
Calculate the energy and the momentum for each photon after the collision.
-
16N.3.HL.TZ0.9a:
The gravitational field strength at 20 Mm above the surface of the Earth is about 0.6 N kg–1. Estimate the time correction per day needed to the time signals, due to the gravitational redshift.
-
16N.3.HL.TZ0.9b:
Suggest, whether your answer to (a) underestimates or overestimates the correction required to the time signal.
-
17M.3.HL.TZ1.5a:
Calculate the potential difference V.
-
17M.3.HL.TZ1.5b:
The proton collides with an antiproton moving with the same speed in the opposite direction. As a result both particles are annihilated and two photons of equal energy are produced.
Determine the momentum of one of the photons.
-
17M.3.HL.TZ1.6a:
Calculate the expected shift in frequency between the emitted and the detected gamma rays.
-
17M.3.HL.TZ1.6b:
Explain whether the detected frequency would be greater or less than the emitted frequency.
-
17M.3.HL.TZ2.6:
A lambda 0 particle at rest decays into a proton p and a pion according to the reaction
0 → p + –
where the rest energy of p = 938 MeV and the rest energy of – = 140 MeV.
The speed of the pion after the decay is 0.579c. For this speed = 1.2265. Calculate the speed of the proton.
-
17M.3.HL.TZ2.7a.i:
State what is meant by the event horizon of a black hole.
-
17M.3.HL.TZ2.7a.ii:
Show that the surface area A of the sphere corresponding to the event horizon is given by
.
-
17M.3.HL.TZ2.7a.iii:
Suggest why the surface area of the event horizon can never decrease.
-
17M.3.HL.TZ2.7b:
The diagram shows a box that is falling freely in the gravitational field of a planet.
A photon of frequency f is emitted from the floor of the box and is received at the ceiling. State and explain the frequency of the photon measured at the ceiling.
-
17N.3.HL.TZ0.7a:
Determine the rest mass of the particle.
-
17N.3.HL.TZ0.7b:
Determine, using your answer to (a), the initial speed of the particle.
-
17N.3.HL.TZ0.8a:
Outline why the clock near the black hole runs slowly compared to a clock close to the distant observer.
-
17N.3.HL.TZ0.8b:
Calculate the number of ticks detected in 10 ks by the distant observer.
-
18M.3.HL.TZ1.6a.ii:
show that the energy of the pion is about 140 MeV.
-
18M.3.HL.TZ1.6b:
State the rest mass of the pion with an appropriate unit.
-
18M.3.HL.TZ1.7a:
Calculate the shift in frequency observed by A in terms of Δf.
-
18M.3.HL.TZ1.7b:
Calculate the gravitational field strength on the surface of planet X.
The following data is given:
Δf = 170 Hz.
The distance between observer A and B is 10 km.
-
18M.3.HL.TZ1.7c:
Observer A now sends a beam of light initially parallel to the surface of the planet.

Explain why the path of the light is curved.
-
18M.3.HL.TZ2.6a:
Calculate the gamma (γ) factor for one of the protons.
-
18M.3.HL.TZ2.6b.i:
Determine, in terms of MeV c–1, the momentum of the pion.
-
18M.3.HL.TZ2.6b.ii:
The diagram shows the paths of the incident protons together with the proton and neutron created in the interaction. On the diagram, draw the path of the pion.
-
18M.3.HL.TZ2.7a.i:
Outline what is meant by the event horizon of a black hole.
-
18M.3.HL.TZ2.7a.ii:
Calculate the distance of the event horizon of the black hole from its centre.
Mass of Sun = 2 × 1030 kg
-
18M.3.HL.TZ2.7b:
Star S-2 is in an elliptical orbit around a black hole. The distance of S-2 from the centre of the black hole varies between a few light-hours and several light-days. A periodic event on S-2 occurs every 5.0 s.

Discuss how the time for the periodic event as measured by an observer on the Earth changes with the orbital position of S-2.
-
18N.3.HL.TZ0.6a:
Show that the momentum of the electron is 1.41 MeV c–1.
- 18N.3.HL.TZ0.6b.i: Explain the origin of each equation.
- 18N.3.HL.TZ0.6b.ii: Calculate, in MeV c–1, p1 and p2.
- 18N.3.HL.TZ0.7a.i: State what is meant by the event horizon of a black hole.
-
18N.3.HL.TZ0.7a.ii:
The mass of the black hole is 4.0 × 1036 kg. Calculate the Schwarzschild radius of the black hole.
-
18N.3.HL.TZ0.7b:
The probe is stationary above the event horizon of the black hole in (a). The probe sends a radio pulse every 1.0 seconds (as measured by clocks on the probe). The spacecraft receives the pulses every 2.0 seconds (as measured by clocks on the spacecraft). Determine the distance of the probe from the centre of the black hole.
- 19M.3.HL.TZ2.8a: Define total energy.
- 19M.3.HL.TZ2.8bi: Determine the momentum of the proton.
-
19M.3.HL.TZ2.8bii:
Determine the speed of the proton.
-
19M.3.HL.TZ2.8biii:
Calculate the potential difference V.
- 19M.3.HL.TZ2.9a: Explain why a change in frequency is expected for the photon detected at the top of the rocket.
- 19M.3.HL.TZ2.9b: Calculate the frequency change.
-
19M.3.HL.TZ1.6a:
Show that energy is conserved in this decay.
-
19M.3.HL.TZ1.6b:
Calculate the speed of the pion.
- 19M.3.HL.TZ1.7a: State the equivalence principle.
- 19M.3.HL.TZ1.7b.i: State and explain the path of the light ray according to observer X.
- 19M.3.HL.TZ1.7b.ii: State and explain the path of the light ray according to observer Y.
-
19N.3.HL.TZ0.5a(i):
the total energy.
-
19N.3.HL.TZ0.5a(ii):
the speed.
-
19N.3.HL.TZ0.5b:
Determine the rest mass of X.
-
19N.3.HL.TZ0.6a:
Explain why the frequency of the radio waves detected by the observer is lower than .
-
19N.3.HL.TZ0.6b:
The probe emits 20 short pulses of these radio waves every minute, according to a clock in the probe. Calculate the time between pulses as measured by the observer.
- 20N.3.HL.TZ0.6a: Define rest mass.
-
20N.3.HL.TZ0.6b:
Calculate the total energy of the deuterium particle in .
- 20N.3.HL.TZ0.6c: In relativistic reactions the mass of the products may be less than the mass of the reactants....
-
20N.3.HL.TZ0.7a:
Calculate the fractional change in frequency of the gamma rays at the detector.
-
20N.3.HL.TZ0.7b(i):
Explain the cause of the frequency shift for the gamma rays in your answer in (a) in the Earth’s gravitational field.
-
20N.3.HL.TZ0.7b(ii):
Explain the cause of the frequency shift for the gamma rays in your answer in (a) if the tower and detector were accelerating towards the gamma rays in free space.
