DP Physics Questionbank

Option A: Relativity (Additional higher level option topics)
Description
Overview of essential ideas for this option
A.4: The relativity of space and time requires new definitions for energy and momentum in order to preserve the conserved nature of these laws.
A.5: General relativity is applied to bring together fundamental concepts of mass, space and time in order to describe the fate of the universe.
Directly related questions
-
16N.3.HL.TZ0.8c:
Calculate the energy and the momentum for each photon after the collision.
-
16N.3.HL.TZ0.9b:
Suggest, whether your answer to (a) underestimates or overestimates the correction required to the time signal.
-
16N.3.HL.TZ0.8b:
Determine the speed of the incoming electron.
-
16N.3.HL.TZ0.9a:
The gravitational field strength at 20 Mm above the surface of the Earth is about 0.6 N kg–1. Estimate the time correction per day needed to the time signals, due to the gravitational redshift.
- 16N.3.HL.TZ0.8a: Explain, in terms of a conservation law, why two photons need to be created.
-
17M.3.HL.TZ2.7a.i:
State what is meant by the event horizon of a black hole.
-
17M.3.HL.TZ1.5a:
Calculate the potential difference V.
-
17M.3.HL.TZ1.6b:
Explain whether the detected frequency would be greater or less than the emitted frequency.
-
17M.3.HL.TZ2.7a.iii:
Suggest why the surface area of the event horizon can never decrease.
-
17M.3.HL.TZ1.6a:
Calculate the expected shift in frequency between the emitted and the detected gamma rays.
-
17M.3.HL.TZ2.6:
A lambda 0 particle at rest decays into a proton p and a pion according to the reaction
0 → p + –
where the rest energy of p = 938 MeV and the rest energy of – = 140 MeV.
The speed of the pion after the decay is 0.579c. For this speed = 1.2265. Calculate the speed of the proton.
-
17M.3.HL.TZ2.7a.ii:
Show that the surface area A of the sphere corresponding to the event horizon is given by
.
-
17M.3.HL.TZ1.5b:
The proton collides with an antiproton moving with the same speed in the opposite direction. As a result both particles are annihilated and two photons of equal energy are produced.
Determine the momentum of one of the photons.
-
17M.3.HL.TZ2.7b:
The diagram shows a box that is falling freely in the gravitational field of a planet.
A photon of frequency f is emitted from the floor of the box and is received at the ceiling. State and explain the frequency of the photon measured at the ceiling.
-
20N.3.HL.TZ0.6b:
Calculate the total energy of the deuterium particle in .
-
20N.3.HL.TZ0.7b(ii):
Explain the cause of the frequency shift for the gamma rays in your answer in (a) if the tower and detector were accelerating towards the gamma rays in free space.
- 20N.3.HL.TZ0.6c: In relativistic reactions the mass of the products may be less than the mass of the reactants....
-
20N.3.HL.TZ0.7b(i):
Explain the cause of the frequency shift for the gamma rays in your answer in (a) in the Earth’s gravitational field.
-
20N.3.HL.TZ0.7a:
Calculate the fractional change in frequency of the gamma rays at the detector.
- 20N.3.HL.TZ0.6a: Define rest mass.
-
17N.3.HL.TZ0.8a:
Outline why the clock near the black hole runs slowly compared to a clock close to the distant observer.
-
17N.3.HL.TZ0.7a:
Determine the rest mass of the particle.
-
17N.3.HL.TZ0.7b:
Determine, using your answer to (a), the initial speed of the particle.
-
17N.3.HL.TZ0.8b:
Calculate the number of ticks detected in 10 ks by the distant observer.
-
18M.3.HL.TZ1.6b:
State the rest mass of the pion with an appropriate unit.
-
18M.3.HL.TZ1.7c:
Observer A now sends a beam of light initially parallel to the surface of the planet.
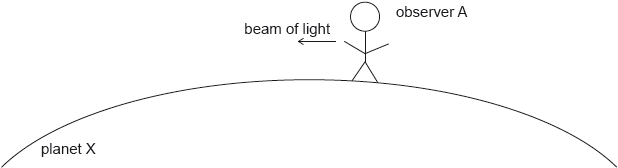
Explain why the path of the light is curved.
-
18M.3.HL.TZ1.6a.ii:
show that the energy of the pion is about 140 MeV.
-
18M.3.HL.TZ1.7a:
Calculate the shift in frequency observed by A in terms of Δf.
-
18M.3.HL.TZ1.7b:
Calculate the gravitational field strength on the surface of planet X.
The following data is given:
Δf = 170 Hz.
The distance between observer A and B is 10 km.
-
18M.3.HL.TZ2.6a:
Calculate the gamma (γ) factor for one of the protons.
-
18M.3.HL.TZ2.6b.i:
Determine, in terms of MeV c–1, the momentum of the pion.
-
18M.3.HL.TZ2.6b.ii:
The diagram shows the paths of the incident protons together with the proton and neutron created in the interaction. On the diagram, draw the path of the pion.
-
18M.3.HL.TZ2.7a.i:
Outline what is meant by the event horizon of a black hole.
-
18M.3.HL.TZ2.7a.ii:
Calculate the distance of the event horizon of the black hole from its centre.
Mass of Sun = 2 × 1030 kg
-
18M.3.HL.TZ2.7b:
Star S-2 is in an elliptical orbit around a black hole. The distance of S-2 from the centre of the black hole varies between a few light-hours and several light-days. A periodic event on S-2 occurs every 5.0 s.
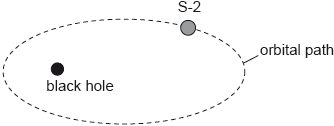
Discuss how the time for the periodic event as measured by an observer on the Earth changes with the orbital position of S-2.
- 18N.3.HL.TZ0.6b.i: Explain the origin of each equation.
- 18N.3.HL.TZ0.7a.i: State what is meant by the event horizon of a black hole.
-
18N.3.HL.TZ0.7a.ii:
The mass of the black hole is 4.0 × 1036 kg. Calculate the Schwarzschild radius of the black hole.
-
18N.3.HL.TZ0.6a:
Show that the momentum of the electron is 1.41 MeV c–1.
- 18N.3.HL.TZ0.6b.ii: Calculate, in MeV c–1, p1 and p2.
-
18N.3.HL.TZ0.7b:
The probe is stationary above the event horizon of the black hole in (a). The probe sends a radio pulse every 1.0 seconds (as measured by clocks on the probe). The spacecraft receives the pulses every 2.0 seconds (as measured by clocks on the spacecraft). Determine the distance of the probe from the centre of the black hole.
- 19M.3.HL.TZ2.8bi: Determine the momentum of the proton.
- 19M.3.HL.TZ2.8a: Define total energy.
-
19M.3.HL.TZ2.8bii:
Determine the speed of the proton.
-
19M.3.HL.TZ2.8biii:
Calculate the potential difference V.
-
19M.3.HL.TZ1.6a:
Show that energy is conserved in this decay.
- 19M.3.HL.TZ1.7b.i: State and explain the path of the light ray according to observer X.
-
19M.3.HL.TZ1.6b:
Calculate the speed of the pion.
- 19M.3.HL.TZ1.7a: State the equivalence principle.
- 19M.3.HL.TZ1.7b.ii: State and explain the path of the light ray according to observer Y.
- 19M.3.HL.TZ2.9b: Calculate the frequency change.
- 19M.3.HL.TZ2.9a: Explain why a change in frequency is expected for the photon detected at the top of the rocket.
-
19N.3.HL.TZ0.5a(i):
the total energy.
-
19N.3.HL.TZ0.5a(ii):
the speed.
-
19N.3.HL.TZ0.5b:
Determine the rest mass of X.
-
19N.3.HL.TZ0.6a:
Explain why the frequency of the radio waves detected by the observer is lower than .
-
19N.3.HL.TZ0.6b:
The probe emits 20 short pulses of these radio waves every minute, according to a clock in the probe. Calculate the time between pulses as measured by the observer.
Sub sections and their related questions
A.4 – Relativistic mechanics (HL only)
- 16N.3.HL.TZ0.8a: Explain, in terms of a conservation law, why two photons need to be created.
-
16N.3.HL.TZ0.8b:
Determine the speed of the incoming electron.
-
16N.3.HL.TZ0.8c:
Calculate the energy and the momentum for each photon after the collision.
-
17M.3.HL.TZ1.5a:
Calculate the potential difference V.
-
17M.3.HL.TZ1.5b:
The proton collides with an antiproton moving with the same speed in the opposite direction. As a result both particles are annihilated and two photons of equal energy are produced.
Determine the momentum of one of the photons.
-
17M.3.HL.TZ2.6:
A lambda 0 particle at rest decays into a proton p and a pion according to the reaction
0 → p + –
where the rest energy of p = 938 MeV and the rest energy of – = 140 MeV.
The speed of the pion after the decay is 0.579c. For this speed = 1.2265. Calculate the speed of the proton.
-
17N.3.HL.TZ0.7a:
Determine the rest mass of the particle.
-
17N.3.HL.TZ0.7b:
Determine, using your answer to (a), the initial speed of the particle.
-
18M.3.HL.TZ1.6a.ii:
show that the energy of the pion is about 140 MeV.
-
18M.3.HL.TZ1.6b:
State the rest mass of the pion with an appropriate unit.
-
18M.3.HL.TZ2.6a:
Calculate the gamma (γ) factor for one of the protons.
-
18M.3.HL.TZ2.6b.i:
Determine, in terms of MeV c–1, the momentum of the pion.
-
18M.3.HL.TZ2.6b.ii:
The diagram shows the paths of the incident protons together with the proton and neutron created in the interaction. On the diagram, draw the path of the pion.
-
18N.3.HL.TZ0.6a:
Show that the momentum of the electron is 1.41 MeV c–1.
- 18N.3.HL.TZ0.6b.i: Explain the origin of each equation.
- 18N.3.HL.TZ0.6b.ii: Calculate, in MeV c–1, p1 and p2.
- 19M.3.HL.TZ2.8a: Define total energy.
- 19M.3.HL.TZ2.8bi: Determine the momentum of the proton.
-
19M.3.HL.TZ2.8bii:
Determine the speed of the proton.
-
19M.3.HL.TZ2.8biii:
Calculate the potential difference V.
-
19M.3.HL.TZ1.6a:
Show that energy is conserved in this decay.
-
19M.3.HL.TZ1.6b:
Calculate the speed of the pion.
-
19N.3.HL.TZ0.5a(i):
the total energy.
-
19N.3.HL.TZ0.5a(ii):
the speed.
-
19N.3.HL.TZ0.5b:
Determine the rest mass of X.
- 20N.3.HL.TZ0.6a: Define rest mass.
-
20N.3.HL.TZ0.6b:
Calculate the total energy of the deuterium particle in .
- 20N.3.HL.TZ0.6c: In relativistic reactions the mass of the products may be less than the mass of the reactants....
A.5 – General relativity (HL only)
-
16N.3.HL.TZ0.9a:
The gravitational field strength at 20 Mm above the surface of the Earth is about 0.6 N kg–1. Estimate the time correction per day needed to the time signals, due to the gravitational redshift.
-
16N.3.HL.TZ0.9b:
Suggest, whether your answer to (a) underestimates or overestimates the correction required to the time signal.
-
17M.3.HL.TZ1.6a:
Calculate the expected shift in frequency between the emitted and the detected gamma rays.
-
17M.3.HL.TZ1.6b:
Explain whether the detected frequency would be greater or less than the emitted frequency.
-
17M.3.HL.TZ2.7a.i:
State what is meant by the event horizon of a black hole.
-
17M.3.HL.TZ2.7a.ii:
Show that the surface area A of the sphere corresponding to the event horizon is given by
.
-
17M.3.HL.TZ2.7a.iii:
Suggest why the surface area of the event horizon can never decrease.
-
17M.3.HL.TZ2.7b:
The diagram shows a box that is falling freely in the gravitational field of a planet.
A photon of frequency f is emitted from the floor of the box and is received at the ceiling. State and explain the frequency of the photon measured at the ceiling.
-
17N.3.HL.TZ0.8a:
Outline why the clock near the black hole runs slowly compared to a clock close to the distant observer.
-
17N.3.HL.TZ0.8b:
Calculate the number of ticks detected in 10 ks by the distant observer.
-
18M.3.HL.TZ1.7a:
Calculate the shift in frequency observed by A in terms of Δf.
-
18M.3.HL.TZ1.7b:
Calculate the gravitational field strength on the surface of planet X.
The following data is given:
Δf = 170 Hz.
The distance between observer A and B is 10 km.
-
18M.3.HL.TZ1.7c:
Observer A now sends a beam of light initially parallel to the surface of the planet.

Explain why the path of the light is curved.
-
18M.3.HL.TZ2.7a.i:
Outline what is meant by the event horizon of a black hole.
-
18M.3.HL.TZ2.7a.ii:
Calculate the distance of the event horizon of the black hole from its centre.
Mass of Sun = 2 × 1030 kg
-
18M.3.HL.TZ2.7b:
Star S-2 is in an elliptical orbit around a black hole. The distance of S-2 from the centre of the black hole varies between a few light-hours and several light-days. A periodic event on S-2 occurs every 5.0 s.

Discuss how the time for the periodic event as measured by an observer on the Earth changes with the orbital position of S-2.
- 18N.3.HL.TZ0.7a.i: State what is meant by the event horizon of a black hole.
-
18N.3.HL.TZ0.7a.ii:
The mass of the black hole is 4.0 × 1036 kg. Calculate the Schwarzschild radius of the black hole.
-
18N.3.HL.TZ0.7b:
The probe is stationary above the event horizon of the black hole in (a). The probe sends a radio pulse every 1.0 seconds (as measured by clocks on the probe). The spacecraft receives the pulses every 2.0 seconds (as measured by clocks on the spacecraft). Determine the distance of the probe from the centre of the black hole.
- 19M.3.HL.TZ2.9a: Explain why a change in frequency is expected for the photon detected at the top of the rocket.
- 19M.3.HL.TZ2.9b: Calculate the frequency change.
- 19M.3.HL.TZ1.7a: State the equivalence principle.
- 19M.3.HL.TZ1.7b.i: State and explain the path of the light ray according to observer X.
- 19M.3.HL.TZ1.7b.ii: State and explain the path of the light ray according to observer Y.
-
19N.3.HL.TZ0.6a:
Explain why the frequency of the radio waves detected by the observer is lower than .
-
19N.3.HL.TZ0.6b:
The probe emits 20 short pulses of these radio waves every minute, according to a clock in the probe. Calculate the time between pulses as measured by the observer.
-
20N.3.HL.TZ0.7a:
Calculate the fractional change in frequency of the gamma rays at the detector.
-
20N.3.HL.TZ0.7b(i):
Explain the cause of the frequency shift for the gamma rays in your answer in (a) in the Earth’s gravitational field.
-
20N.3.HL.TZ0.7b(ii):
Explain the cause of the frequency shift for the gamma rays in your answer in (a) if the tower and detector were accelerating towards the gamma rays in free space.
