| Date | November 2015 | Marks available | 2 | Reference code | 15N.2.hl.TZ0.4 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Solve | Question number | 4 | Adapted from | N/A |
Question
A function is defined by \(f(x) = A\sin (Bx) + C,{\text{ }} - \pi \le x \le \pi \), where \(A,{\text{ }}B,{\text{ }}C \in \mathbb{Z}\). The following diagram represents the graph of \(y = f(x)\).
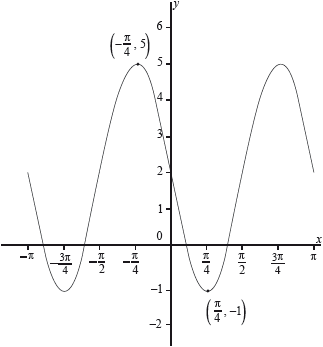
Find the value of
(i) \(A\);
(ii) \(B\);
(iii) \(C\).
Solve \(f(x) = 3\) for \(0 \le x \le \pi \).
Markscheme
(i) \(A = - 3\) A1
(ii) period \( = \frac{\pi }{B}\) (M1)
\(B = 2\) A1
Note: Award as above for \(A = 3\) and \(B = - 2\).
(iii) \(C = 2\) A1
[4 marks]
\(x = 1.74,{\text{ }}2.97\;\;\;\left( {x = \frac{1}{2}\left( {\pi + \arcsin \frac{1}{3}} \right),{\text{ }}\frac{1}{2}\left( {2\pi - \arcsin \frac{1}{3}} \right)} \right)\) (M1)A1
Note: Award (M1)A0 if extra correct solutions eg \(( - 1.40,{\text{ }} - 0.170)\) are given outside the domain \(0 \le x \le \pi \). Do not award FT in (b).
[2 marks]
Total [6 marks]

