| Date | November 2017 | Marks available | 3 | Reference code | 17N.2.hl.TZ0.11 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Solve | Question number | 11 | Adapted from | N/A |
Question
Consider the function \(f(x) = 2{\sin ^2}x + 7\sin 2x + \tan x - 9,{\text{ }}0 \leqslant x < \frac{\pi }{2}\).
Let \(u = \tan x\).
Determine an expression for \(f’(x)\) in terms of \(x\).
Sketch a graph of \(y = f’(x)\) for \(0 \leqslant x < \frac{\pi }{2}\).
Find the \(x\)-coordinate(s) of the point(s) of inflexion of the graph of \(y = f(x)\), labelling these clearly on the graph of \(y = f’(x)\).
Express \(\sin x\) in terms of \(\mu \).
Express \(\sin 2x\) in terms of \(u\).
Hence show that \(f(x) = 0\) can be expressed as \({u^3} - 7{u^2} + 15u - 9 = 0\).
Solve the equation \(f(x) = 0\), giving your answers in the form \(\arctan k\) where \(k \in \mathbb{Z}\).
Markscheme
\(f’(x) = 4\sin x\cos x + 14\cos 2x + {\sec ^2}x\) (or equivalent) (M1)A1
[2 marks]
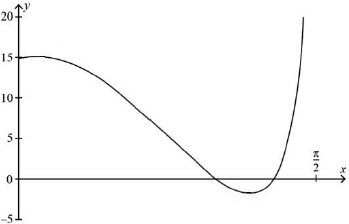 A1A1A1A1
A1A1A1A1
Note: Award A1 for correct behaviour at \(x = 0\), A1 for correct domain and correct behaviour for \(x \to \frac{\pi }{2}\), A1 for two clear intersections with \(x\)-axis and minimum point, A1 for clear maximum point.
[4 marks]
\(x = 0.0736\) A1
\(x = 1.13\) A1
[2 marks]
attempt to write \(\sin x\) in terms of \(u\) only (M1)
\(\sin x = \frac{u}{{\sqrt {1 + {u^2}} }}\) A1
[2 marks]
\(\cos x = \frac{1}{{\sqrt {1 + {u^2}} }}\) (A1)
attempt to use \(\sin 2x = 2\sin x\cos x{\text{ }}\left( { = 2\frac{u}{{\sqrt {1 + {u^2}} }}\frac{1}{{\sqrt {1 + {u^2}} }}} \right)\) (M1)
\(\sin 2x = \frac{{2u}}{{1 + {u^2}}}\) A1
[3 marks]
\(2{\sin ^2}x + 7\sin 2x + \tan x - 9 = 0\)
\(\frac{{2{u^2}}}{{1 + {u^2}}} + \frac{{14u}}{{1 + {u^2}}} + u - 9{\text{ }}( = 0)\) M1
\(\frac{{2{u^2} + 14u + u(1 + {u^2}) - 9(1 + {u^2})}}{{1 + {u^2}}} = 0\) (or equivalent) A1
\({u^3} - 7{u^2} + 15u - 9 = 0\) AG
[2 marks]
\(u = 1\) or \(u = 3\) (M1)
\(x = \arctan (1)\) A1
\(x = \arctan (3)\) A1
Note: Only accept answers given the required form.
[3 marks]

