| Date | May 2014 | Marks available | 3 | Reference code | 14M.1.hl.TZ2.5 |
| Level | HL only | Paper | 1 | Time zone | TZ2 |
| Command term | Solve | Question number | 5 | Adapted from | N/A |
Question
Sketch the graph of \(y = \left| {\cos \left( {\frac{x}{4}} \right)} \right|\) for \(0 \leqslant x \leqslant 8\pi \).
Solve \(\left| {\cos \left( {\frac{x}{4}} \right)} \right| = \frac{1}{2}\) for \(0 \leqslant x \leqslant 8\pi \).
Markscheme
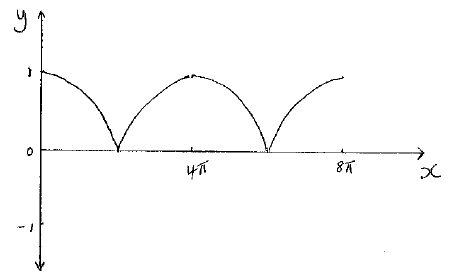 A1A1
A1A1
Note: Award A1 for correct shape and A1 for correct domain and range.
[2 marks]
\(\left| {\cos \left( {\frac{x}{4}} \right)} \right| = \frac{1}{2}\)
\(x = \frac{{4\pi }}{3}\) A1
attempting to find any other solutions M1
Note: Award (M1) if at least one of the other solutions is correct (in radians or degrees) or clear use of symmetry is seen.
\(x = 8\pi - \frac{{4\pi }}{3} = \frac{{20 \pi }}{3}\)
\(x = 4\pi - \frac{{4\pi }}{3} = \frac{{8\pi }}{3}\)
\(x = 4\pi + \frac{{4\pi }}{3} = \frac{{16\pi }}{3}\) A1
Note: Award A1 for all other three solutions correct and no extra solutions.
Note: If working in degrees, then max A0M1A0.
[3 marks]

