| Date | May 2017 | Marks available | 3 | Reference code | 17M.2.hl.TZ1.8 |
| Level | HL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
A water trough which is 10 metres long has a uniform cross-section in the shape of a semicircle with radius 0.5 metres. It is partly filled with water as shown in the following diagram of the cross-section. The centre of the circle is O and the angle KOL is \(\theta \) radians.
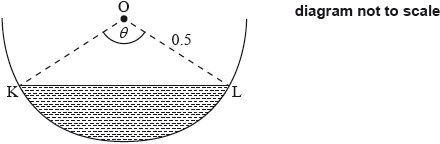
The volume of water is increasing at a constant rate of \(0.0008{\text{ }}{{\text{m}}^3}{{\text{s}}^{ - 1}}\).
Find an expression for the volume of water \(V{\text{ }}({{\text{m}}^3})\) in the trough in terms of \(\theta \).
Calculate \(\frac{{{\text{d}}\theta }}{{{\text{d}}t}}\) when \(\theta = \frac{\pi }{3}\).
Markscheme
area of segment \( = \frac{1}{2} \times {0.5^2} \times (\theta - \sin \theta )\) M1A1
\(V = {\text{area of segment}} \times 10\)
\(V = \frac{5}{4}(\theta - \sin \theta )\) A1
[3 marks]
METHOD 1
\(\frac{{{\text{d}}V}}{{{\text{d}}t}} = \frac{5}{4}(1 - \cos \theta )\frac{{{\text{d}}\theta }}{{{\text{d}}t}}\) M1A1
\(0.0008 = \frac{5}{4}\left( {1 - \cos \frac{\pi }{3}} \right)\frac{{{\text{d}}\theta }}{{{\text{d}}t}}\) (M1)
\(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = 0.00128{\text{ }}({\text{rad}}\,{s^{ - 1}})\) A1
METHOD 2
\(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{{{\text{d}}\theta }}{{{\text{d}}V}} \times \frac{{{\text{d}}V}}{{{\text{d}}t}}\) (M1)
\(\frac{{{\text{d}}V}}{{{\text{d}}\theta }} = \frac{5}{4}(1 - \cos \theta )\) A1
\(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{{4 \times 0.0008}}{{5\left( {1 - \cos \frac{\pi }{3}} \right)}}\) (M1)
\(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = 0.00128\left( {\frac{4}{{3125}}} \right)({\text{rad }}{s^{ - 1}})\) A1
[4 marks]

