| Date | November 2017 | Marks available | 4 | Reference code | 17N.2.hl.TZ0.3 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
This diagram shows a metallic pendant made out of four equal sectors of a larger circle of radius \({\text{OB}} = 9{\text{ cm}}\) and four equal sectors of a smaller circle of radius \({\text{OA}} = 3{\text{ cm}}\).
The angle \({\text{BOC}} = \) 20°.
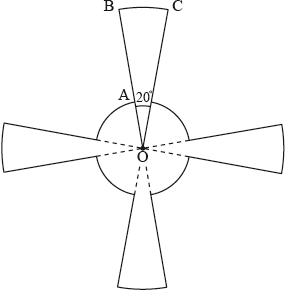
Find the area of the pendant.
Markscheme
METHOD 1
area = (four sector areas radius 9) + (four sector areas radius 3) (M1)
\( = 4\left( {\frac{1}{2}{9^2}\frac{\pi }{9}} \right) + 4\left( {\frac{1}{2}{3^2}\frac{{7\pi }}{{18}}} \right)\) (A1)(A1)
\( = 18\pi + 7\pi \)
\( = 25\pi {\text{ }}( = 78.5{\text{ c}}{{\text{m}}^2})\) A1
METHOD 2
area =
(area of circle radius 3) + (four sector areas radius 9) – (four sector areas radius 3) (M1)
\(\pi {3^2} + 4\left( {\frac{1}{2}{9^2}\frac{\pi }{9}} \right) - 4\left( {\frac{1}{2}{3^2}\frac{\pi }{9}} \right)\) (A1)(A1)
Note: Award A1 for the second term and A1 for the third term.
\( = 9\pi + 18\pi - 2\pi \)
\( = 25\pi {\text{ }}( = {\text{ }}78.5{\text{ c}}{{\text{m}}^2})\) A1
Note: Accept working in degrees.
[4 marks]

