| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.hl.TZ1.1 |
| Level | HL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
The logo, for a company that makes chocolate, is a sector of a circle of radius \(2\) cm, shown as shaded in the diagram. The area of the logo is \(3\pi {\text{ c}}{{\text{m}}^2}\).
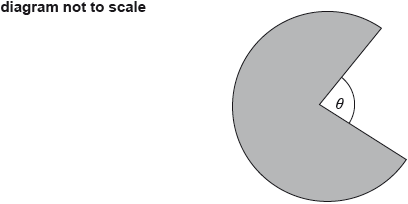
Find, in radians, the value of the angle \(\theta \), as indicated on the diagram.
Find the total length of the perimeter of the logo.
Markscheme
METHOD 1
\({\text{area}} = \pi {2^2} - \frac{1}{2}{2^2}\theta \;\;\;( = 3\pi )\) M1A1
Note: Award M1 for using area formula.
\( \Rightarrow 2\theta = \pi \Rightarrow \theta = \frac{\pi }{2}\) A1
Note: Degrees loses final A1
METHOD 2
let \(x = 2\pi - \theta \)
\({\text{area}} = \frac{1}{2}{2^2}x\;\;\;( = 3\pi )\) M1
\( \Rightarrow x = \frac{3}{2}\pi \) A1
\( \Rightarrow \theta = \frac{\pi }{2}\) A1
METHOD 3
Area of circle is \(4\pi \) A1
Shaded area is \(\frac{3}{4}\) of the circle (R1)
\( \Rightarrow \theta = \frac{\pi }{2}\) A1
[3 marks]
\({\text{arc length}} = 2\frac{{3\pi }}{2}\) A1
\({\text{perimeter}} = 2\frac{{3\pi }}{2} + 2 \times 2\)
\( = 3\pi + 4\) A1
[2 marks]
Total [5 marks]
Examiners report
Good methods. Some candidates found the larger angle.
Generally good, some forgot the radii.

