| Date | May 2014 | Marks available | 6 | Reference code | 14M.2.hl.TZ2.4 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
The following diagram shows two intersecting circles of radii 4 cm and 3 cm. The centre C of the smaller circle lies on the circumference of the bigger circle. O is the centre of the bigger circle and the two circles intersect at points A and B.
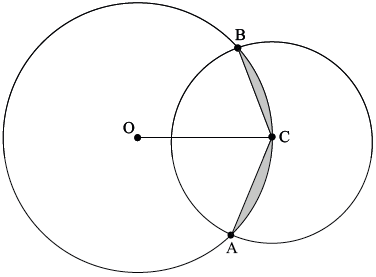
Find:
(a) \({\rm{B\hat OC}}\);
(b) the area of the shaded region.
Markscheme
(a) METHOD 1
\(2{\text{arcsin}}\left( {\frac{{1.5}}{4}} \right)\) M1
\(\alpha = {0.769^c}{\text{ (44.0}}^\circ {\text{)}}\) A1
METHOD 2
using the cosine rule:
\({3^2} = {4^2} + {4^2} - 2(4)(4)\cos \alpha \) M1
\(\alpha = {0.769^c}{\text{ (44.0}}^\circ {\text{)}}\) A1
[2 marks]
(b) one segment
\({{\text{A}}_1} = \frac{1}{2} \times {4^2} \times 0.76879 - \frac{1}{2} \times {4^2}\sin (0.76879)\) M1A1
\( = 0.58819{\text{K}}\) (A1)
\(2{{\text{A}}_1} = 1.18{\text{ }}({\text{c}}{{\text{m}}^2})\) A1
Note: Award M1 only if both sector and triangle are considered.
[4 marks]
Total [6 marks]

