| Date | May 2015 | Marks available | 4 | Reference code | 15M.2.hl.TZ2.8 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | Calculate and Give | Question number | 8 | Adapted from | N/A |
Question
Farmer Bill owns a rectangular field, 10 m by 4 m. Bill attaches a rope to a wooden post at one corner of his field, and attaches the other end to his goat Gruff.
Given that the rope is 5 m long, calculate the percentage of Bill’s field that Gruff is able to graze. Give your answer correct to the nearest integer.
Bill replaces Gruff’s rope with another, this time of length \(a,{\text{ }}4 < a < 10\), so that Gruff can now graze exactly one half of Bill’s field.
Show that \(a\) satisfies the equation
\[{a^2}\arcsin \left( {\frac{4}{a}} \right) + 4\sqrt {{a^2} - 16} = 40.\]
Find the value of \(a\).
Markscheme
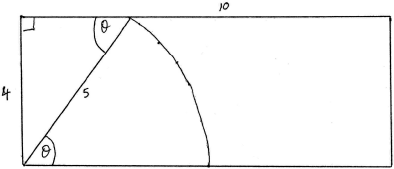
EITHER
area of triangle \( = \frac{1}{2} \times 3 \times 4\;\;\;( = 6)\) A1
area of sector \( = \frac{1}{2}\arcsin \left( {\frac{4}{5}} \right) \times {5^2}\;\;\;( = 11.5911 \ldots )\) A1
OR
\(\int_0^4 {\sqrt {25 - {x^2}} {\text{d}}x} \) M1A1
THEN
total area \( = 17.5911 \ldots {\text{ }}{{\text{m}}^2}\) (A1)
percentage \( = \frac{{17.5911 \ldots }}{{40}} \times 100 = 44\% \) A1
[4 marks]
METHOD 1
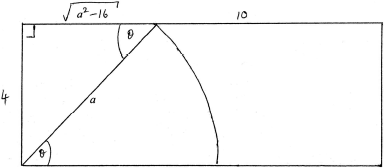
area of triangle \( = \frac{1}{2} \times 4 \times \sqrt {{a^2} - 16} \) A1
\(\theta = \arcsin \left( {\frac{4}{a}} \right)\) (A1)
area of sector \( = \frac{1}{2}{r^2}\theta = \frac{1}{2}{a^2}\arcsin \left( {\frac{4}{a}} \right)\) A1
therefore total area \( = 2\sqrt {{a^2} - 16} + \frac{1}{2}{a^2}\arcsin \left( {\frac{4}{a}} \right) = 20\) A1
rearrange to give: \({a^2}\arcsin \left( {\frac{4}{a}} \right) + 4\sqrt {{a^2} - 16} = 40\) AG
METHOD 2
\(\int_0^4 {\sqrt {{a^2} - {x^2}} {\text{d}}x = 20} \) M1
use substitution \(x = a\sin \theta ,{\text{ }}\frac{{{\text{d}}x}}{{{\text{d}}\theta }} = a\cos \theta \)
\(\int_0^{\arcsin \left( {\frac{4}{a}} \right)} {{a^2}{{\cos }^2}\theta {\text{d}}\theta = 20} \)
\(\frac{{{a^2}}}{2}\int_0^{\arcsin \left( {\frac{4}{a}} \right)} {(\cos 2\theta + 1){\text{d}}\theta = 20} \) M1
\({a^2}\left[ {\left( {\frac{{\sin 2\theta }}{2} + \theta } \right)} \right]_0^{\arcsin \left( {\frac{4}{a}} \right)} = 40\) A1
\({a^2}\left[ {(\sin \theta \cos \theta + \theta } \right]_0^{\arcsin \left( {\frac{4}{a}} \right)} = 40\)
\({a^2}\arcsin \left( {\frac{4}{a}} \right) + {a^2}\left( {\frac{4}{a}} \right)\sqrt {\left( {1 - {{\left( {\frac{4}{a}} \right)}^2}} \right)} = 40\) A1
\({a^2}\arcsin \left( {\frac{4}{a}} \right) + 4\sqrt {{a^2} - 16} = 40\) AG
[4 marks]
solving using \({\text{GDC}} \Rightarrow a = 5.53{\text{ cm}}\) A2
[2 marks]
Total [10 marks]

