| Date | November 2015 | Marks available | 4 | Reference code | 15N.1.hl.TZ0.1 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
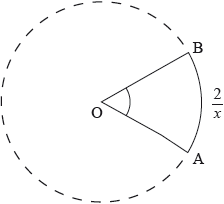
The following diagram shows a sector of a circle where \({\rm{A\hat OB}} = x\) radians and the length of the \({\text{arc AB}} = \frac{2}{x}{\text{ cm}}\).
Given that the area of the sector is \(16{\text{ c}}{{\text{m}}^2}\), find the length of the arc \(AB\).
Markscheme
\({\text{arc length}} = \frac{2}{x} = rx\;\;\;\left( { \Rightarrow r = \frac{2}{{{x^2}}}} \right)\) M1
\(16 = \frac{1}{2}{\left( {\frac{2}{{{x^2}}}} \right)^2}x\;\;\;\left( { \Rightarrow \frac{2}{{{x^3}}} = 16} \right)\) M1
Note: Award M1s for attempts at the use of arc-length and sector-area formulae.
\(x = \frac{1}{2}\) A1
\({\text{arc length}} = {\text{4 (cm)}}\) A1
[4 marks]

