| Date | May 2017 | Marks available | 5 | Reference code | 17M.1.hl.TZ2.9 |
| Level | HL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
Consider the function \(f\) defined by \(f(x) = {x^2} - {a^2},{\text{ }}x \in \mathbb{R}\) where \(a\) is a positive constant.
The function \(g\) is defined by \(g(x) = x\sqrt {f(x)} \) for \(\left| x \right| > a\).
Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = f(x)\);
Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \frac{1}{{f(x)}}\);
Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \left| {\frac{1}{{f(x)}}} \right|\).
Find \(\int {f(x)\cos x{\text{d}}x} \).
By finding \(g'(x)\) explain why \(g\) is an increasing function.
Markscheme
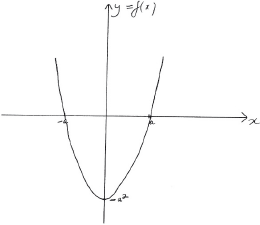
A1 for correct shape
A1 for correct \(x\) and \(y\) intercepts and minimum point
[2 marks]
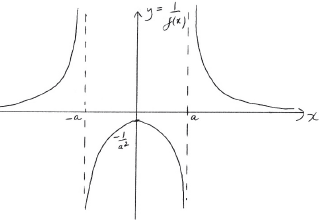
A1 for correct shape
A1 for correct vertical asymptotes
A1 for correct implied horizontal asymptote
A1 for correct maximum point
[??? marks]
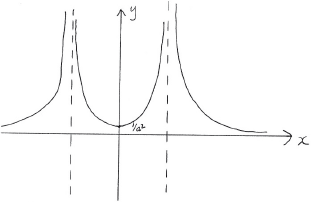
A1 for reflecting negative branch from (ii) in the \(x\)-axis
A1 for correctly labelled minimum point
[2 marks]
EITHER
attempt at integration by parts (M1)
\(\int {({x^2} - {a^2})\cos x{\text{d}}x = ({x^2} - {a^2})\sin x - \int {2x\sin x{\text{d}}x} } \) A1A1
\( = ({x^2} - {a^2})\sin x - 2\left[ { - x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = ({x^2} - {a^2})\sin x + 2x\cos - 2\sin x + c\) A1
OR
\(\int {({x^2} - {a^2})\cos x{\text{d}}x = \int {{x^2}\cos x{\text{d}}x - \int {{a^2}\cos x{\text{d}}x} } } \)
attempt at integration by parts (M1)
\(\int {{x^2}\cos x{\text{d}}x = {x^2}\sin x - \int {2x\sin x{\text{d}}x} } \) A1A1
\( = {x^2}\sin x - 2\left[ { - x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = {x^2}\sin x + 2x\cos x - 2\sin x\)
\( - \int {{a^2}\cos x{\text{d}}x = - {a^2}\sin x} \)
\(\int {({x^2} - {a^2})\cos x{\text{d}}x = ({x^2} - {a^2})\sin x + 2x\cos x - 2\sin x + c} \) A1
[5 marks]
\(g(x) = x{({x^2} - {a^2})^{\frac{1}{2}}}\)
\(g'(x) = {({x^2} - {a^2})^{\frac{1}{2}}} + \frac{1}{2}x{({x^2} - {a^2})^{ - \frac{1}{2}}}(2x)\) M1A1A1
Note: Method mark is for differentiating the product. Award A1 for each correct term.
\(g'(x) = {({x^2} - {a^2})^{\frac{1}{2}}} + {x^2}{({x^2} - {a^2})^{ - \frac{1}{2}}}\)
both parts of the expression are positive hence \(g'(x)\) is positive R1
and therefore \(g\) is an increasing function (for \(\left| x \right| > a\)) AG
[4 marks]

