| Date | May 2016 | Marks available | 2 | Reference code | 16M.2.hl.TZ2.8 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find and Sketch | Question number | 8 | Adapted from | N/A |
Question
A particle moves such that its velocity \(v\,{\text{m}}{{\text{s}}^{ - 1}}\) is related to its displacement \(s\,{\text{m}}\), by the equation \(v(s) = \arctan (\sin s),{\text{ }}0 \leqslant s \leqslant 1\). The particle’s acceleration is \(a\,{\text{m}}{{\text{s}}^{ - 2}}\).
Find the particle’s acceleration in terms of \(s\).
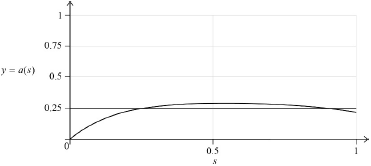
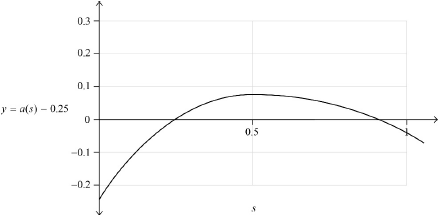
Using an appropriate sketch graph, find the particle’s displacement when its acceleration is \(0.25{\text{ m}}{{\text{s}}^{ - 2}}\).
Markscheme
\(\frac{{{\text{d}}v}}{{{\text{d}}s}} = \frac{{\cos s}}{{{{\sin }^2}s + 1}}\) M1A1
\(a = v\frac{{{\text{d}}v}}{{{\text{d}}s}}\) (M1)
\(a = \frac{{\arctan (\sin s)\cos s}}{{{{\sin }^2}s + 1}}\) A1
[4 marks]
EITHER
 (M1)
(M1)
OR
 (M1)
(M1)
THEN
\(s = 0.296,{\text{ }}0.918{\text{ (m)}}\) A1
[2 marks]
Examiners report
In part (a), a large number of candidates thought that \(\frac{{{\text{d}}v}}{{{\text{d}}t}} = \frac{{{\text{d}}v}}{{{\text{d}}s}}\) rather than \(\frac{{{\text{d}}v}}{{{\text{d}}t}} = \frac{{{\text{d}}s}}{{{\text{d}}t}} \times \frac{{{\text{d}}v}}{{{\text{d}}s}} = v\frac{{{\text{d}}v}}{{{\text{d}}s}}\).
In part (b), quite a few of these candidates then went on to find a value of \(s\) that was outside the domain \(0 \leqslant s \leqslant 1\).

