| Date | May 2015 | Marks available | 4 | Reference code | 15M.2.hl.TZ2.12 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 12 | Adapted from | N/A |
Question
A particle moves in a straight line, its velocity \(v{\text{ m}}{{\text{s}}^{ - 1}}\) at time \(t\) seconds is given by \(v = 9t - 3{t^2},{\text{ }}0 \le t \le 5\).
At time \(t = 0\), the displacement \(s\) of the particle from an origin \(O\) is 3 m.
Find the displacement of the particle when \(t = 4\).
Sketch a displacement/time graph for the particle, \(0 \le t \le 5\), showing clearly where the curve meets the axes and the coordinates of the points where the displacement takes greatest and least values.
For \(t > 5\), the displacement of the particle is given by \(s = a + b\cos \frac{{2\pi t}}{5}\) such that \(s\) is continuous for all \(t \ge 0\).
Given further that \(s = 16.5\) when \(t = 7.5\), find the values of \(a\) and \(b\).
For \(t > 5\), the displacement of the particle is given by \(s = a + b\cos \frac{{2\pi t}}{5}\) such that \(s\) is continuous for all \(t \ge 0\).
Find the times \({t_1}\) and \({t_2}(0 < {t_1} < {t_2} < 8)\) when the particle returns to its starting point.
Markscheme
METHOD 1
\(s = \int {(9t - 3{t^2}){\text{d}}t = \frac{9}{2}{t^2} - {t^3}( + c)} \) (M1)
\(t = 0,{\text{ }}s = 3 \Rightarrow c = 3\) (A1)
\(t = 4 \Rightarrow s = 11\) A1
METHOD 2
\(s = 3 + \int_0^4 {(9t - 3{t^2}){\text{d}}t} \) (M1)(A1)
\(s = 11\) A1
[3 marks]
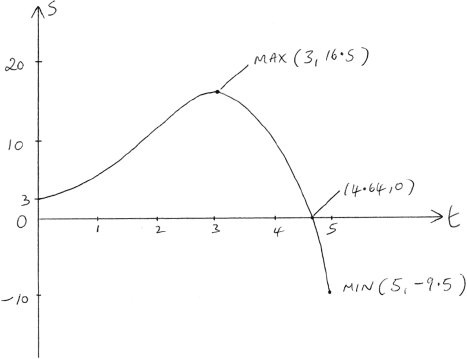
correct shape over correct domain A1
maximum at \((3,{\text{ }}16.5)\) A1
\(t\) intercept at \(4.64\), \(s\) intercept at \(3\) A1
minimum at \((5,{\text{ }} - 9.5)\) A1
[5 marks]
\( - 9.5 = a + b\cos 2\pi \)
\(16.5 = a + b\cos 3\pi \) (M1)
Note: Only award M1 if two simultaneous equations are formed over the correct domain.
\(a = \frac{7}{2}\) A1
\(b = - 13\) A1
[3 marks]
at \({t_1}\):
\(3 + \frac{9}{2}{t^2} - {t^3} = 3\) (M1)
\({t^2}\left( {\frac{9}{2} - t} \right) = 0\)
\({t_1} = \frac{9}{2}\) A1
solving \(\frac{7}{2} - 13\cos \frac{{2\pi t}}{5} = 3\) (M1)
\({\text{GDC}} \Rightarrow {t_2} = 6.22\) A1
Note: Accept graphical approaches.
[4 marks]
Total [15 marks]

