| Date | May 2016 | Marks available | 6 | Reference code | 16M.1.hl.TZ2.1 |
| Level | HL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
The following system of equations represents three planes in space.
\[x + 3y + z = - 1\]
\[x + 2y - 2z = 15\]
\[2x + y - z = 6\]
Find the coordinates of the point of intersection of the three planes.
Markscheme
EITHER
eliminating a variable, \(x\), for example to obtain \(y + 3z = - 16\) and \( - 5y - 3z = 8\) M1A1
attempting to find the value of one variable M1
point of intersection is \(( - 1,{\text{ }}2,{\text{ }} - 6)\) A1A1A1
OR
attempting row reduction of relevant matrix, eg. 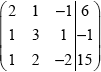 M1
M1
correct matrix with two zeroes in a column, eg. 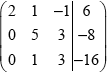 A1
A1
further attempt at reduction M1
point of intersection is \(( - 1,{\text{ }}2,{\text{ }} - 6)\) A1A1A1
Note: Allow solution expressed as \(x = - 1,{\text{ }}y = 2,{\text{ }}z = - 6\) for final A marks.
[6 marks]
Examiners report
This provided a generally easy start for many candidates. Most successful candidates obtained their answer through row reduction of a suitable matrix. Those choosing an alternative method often made slips in their algebra.

