| Date | May 2016 | Marks available | 1 | Reference code | 16M.2.hl.TZ1.7 |
| Level | HL only | Paper | 2 | Time zone | TZ1 |
| Command term | Calculate | Question number | 7 | Adapted from | N/A |
Question
It has been suggested that in rowing competitions the time, \(T\) seconds taken to complete a 2000 m race can be modelled by an equation of the form \(T = a{N^b}\), where \(N\) is the number of rowers in the boat and \(a\) and \(b\) are constants for rowers of a similar standard.
To test this model the times for the finalists in all the 2000 m men’s races at a recent Olympic games were recorded and the mean calculated.
The results are shown in the following table for \(N = 1\) and \(N = 2\).
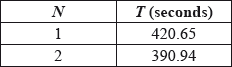
It is now given that the mean time in the final for boats with 8 rowers was 342.08 seconds.
Use these results to find estimates for the value of \(a\) and the value of \(b\). Give your answers to five significant figures.
Use this model to estimate the mean time for the finalists in an Olympic race for boats with 8 rowers. Give your answer correct to two decimal places.
Calculate the error in your estimate as a percentage of the actual value.
Comment on the likely validity of the model as \(N\) increases beyond 8.
Markscheme
\(a = 420.65\) A1
\(390.94 = a \times {2^b}\) M1
\({2^b} = \frac{{390.94}}{{420.65}} = 0.929 \ldots \) A1
\(b = - 0.10567\) A1
[4 marks]
\(N = 8\,\,\,T = 337.67\) A1
Note: Accept 5sf answers between 337.44 and 337.67.
[1 mark]
\(N = 8\) Percentage error 1.29% A1
Note: Accept negative values of the above.
[1 mark]
likely not to be a good fit for larger values of \(N\) R1
likely to be quite a good fit for values close to 8 R1
[2 marks]
Examiners report
Parts (a) to (c) were generally well done, although far too much inaccuracy with basic calculations.
Parts (a) to (c) were generally well done, although far too much inaccuracy with basic calculations.
Parts (a) to (c) were generally well done, although far too much inaccuracy with basic calculations.
Parts (a) to (c) were generally well done, although far too much inaccuracy with basic calculations. Part (d) caused more difficulties as candidates frequently had insufficient analysis to gain the two marks.

