| Date | November 2014 | Marks available | 2 | Reference code | 14N.2.SL.TZ0.3 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Explain | Question number | 3 | Adapted from | N/A |
Question
This question is about radioactive decay.
A nucleus of an iodine isotope, I-131, undergoes radioactive decay to form a nucleus of the nuclide xenon-131. Xe-131 is stable.
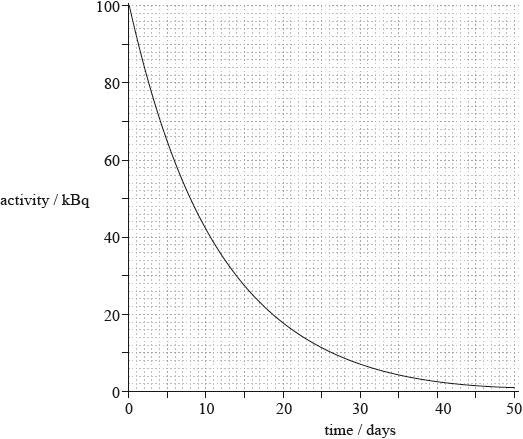
The initial activity of a sample of I-131 is 100 kBq. The subsequent variation of the activity of the sample with time is shown in the graph.
Explain what is meant by an isotope.
Identify the missing entries to complete the nuclear reaction for the decay of I-131.
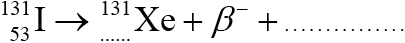
The I-131 can be used for a medical application but only when the activity lies within the range of \((20 \pm 10){\text{ kBq}}\). Determine an estimate for the time during which the iodine can be used.
A different isotope has half the initial activity and double the half-life of I-131. On the graph in (c), sketch the variation of activity with time for this isotope.
Markscheme
same number of protons / atoms of the same element;
different number of neutrons;
54 and antineutrino/\(\bar \nu \); (both needed)
range is 14 to 26 or 14 to 27;
12 or 13 days;
Award [2] if marking points added to the graph.
starts at 50 kBq and approximately exponential decay curve;
half-life is \( \sim {\text{16 days}}\) / line passes through \([16,{\text{ }}25]\) to within a small square;
Examiners report
A variety of good answers.
Many seemed unaware of the antineutrino.
Many candidates were able to determine the answer from the activity graph, but quite a few misunderstood what the question was asking for.
This was done quite well, with most graphs starting at 50Bq and having the required half-life. However, too many candidates did not draw an acceptable exponentially shaped graph.

