| Date | November 2015 | Marks available | 2 | Reference code | 15N.2.SL.TZ0.4 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Determine | Question number | 4 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about the nuclear model of the atom and radioactive decay. Part 2 is about waves.
Part 1 Nuclear model of the atom and radioactive decay
The nuclide radium-226 \(\left( {_{\;{\text{88}}}^{{\text{226}}}{\text{Ra}}} \right)\) decays into an isotope of radon (Rn) by the emission of an alpha particle and a gamma-ray photon.
Part 2 Waves
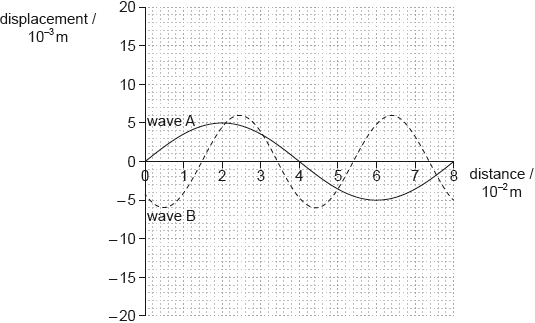
Two waves, A and B, are travelling in opposite directions in a tank of water. The graph shows the variation of displacement of the water surface with distance along the wave at a particular instant.
Outline how the evidence supplied by the Geiger–Marsden experiment supports the nuclear model of the atom.
Outline why classical physics does not permit a model of an electron orbiting the nucleus.
State what is meant by the terms nuclide and isotope.
Nuclide:
Isotope:
Construct the nuclear equation for the decay of radium-226.
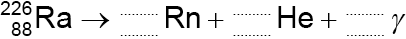
Radium-226 has a half-life of 1600 years. Determine the time, in years, it takes for the activity of radium-226 to fall to \(\frac{1}{{64}}\) of its original activity.
State the amplitude of wave A.
Wave A has a frequency of 9.0 Hz. Calculate the velocity of wave A.
Deduce the frequency of wave B.
State what is meant by the principle of superposition of waves.
On the graph opposite, sketch the wave that results from the superposition of wave A and wave B at that instant.
Markscheme
most undeflected/pass straight through;
hence mostly empty space;
few deflected; (allow “bent”, “reflect”, “bounce back” etc)
hence small dense nucleus;
positive / positively charged;
electron accelerated / mention of centripetal force;
should radiate EM waves/energy;
and spiral into the nucleus;
nuclide: nucleus characterized by specified number of protons and neutrons/its constituents;
isotope: nuclide with same number of protons / same element and different numbers of nucleons/neutrons;
\(_{\;86}^{222}{\text{Rn}}\);
\(_2^4{\text{He}}\) or \(_0^0\gamma \);
top and bottom numbers balanced correctly;
6 half-lives occurred;
9600 years;
Award [2] for a bald correct answer.
5 mm or 5.0 mm; units are required
Allow other units, eg: 5/5.0 \( \times \) 10–3 m.
wavelength \( = {\text{8.0 cm}}\) or 8 cm; (accept clear substitution in MP2 for this mark)
\(v = (f\lambda = ){\text{ }}9 \times 8 = 72{\text{ cm}}\,{{\text{s}}^{ - 1}}\); units are required
Award [2] for a bald correct answer.
wavelength \( = 3.9{\text{ (cm)}}\); (accept answers in the range of 3.8 to 4.0 (cm))
frequency \( = \left( {\frac{{72}}{{3.9}} = } \right){\text{ 18}}\);
Hz or \({{\text{s}}^{ - 1}}\);
Award [3] for a bald correct answer that includes unit.
when two or more waves (of the same nature) meet/interfere / OWTTE;
the resultant displacement is the (vector) sum of their individual displacements; } (do not allow constructive or destructive interference as answer to this point)
Do not accept “amplitude” for “displacement” anywhere in answer.
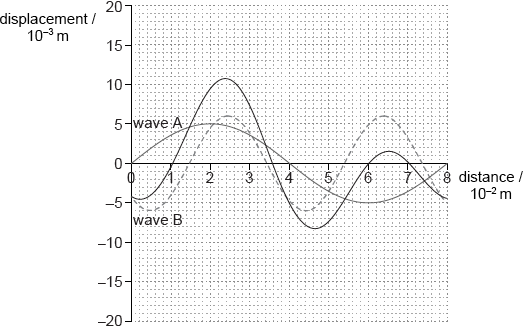
start and end points correct (equal B) and crossing points on distance axis correct \({\text{(1, 3.6, 6, 7)}}\);
peaks and troughs at \({\text{(2.4, 11)}}\) \({\text{(4.6, }}-{\text{8)}}\) \({\text{(6.5, 1.5)}}\);
general shape correct as in example; } (maximum and minimum must be alternating +/–)
All tolerances ± 1 square.
Examiners report
This was generally well done, but too many candidates focused upon a description of the experiment rather than the evidence it provided.
Very poorly done.
The word nuclide refers to a nucleus with a specific number of protons and neutrons. Very few candidates understood this. They were, however, mostly able to show a clear understanding of what an isotope was.
No problem for the majority of candidates.
Most candidates were able to give the correct answer.
This was well done – an omission of the vital unit (so that the examiner can confirm the reading) was not too common.
This part was well done.
This part was well done.
Many candidates described the meeting or interference of two waves, however, a considerable number went on to confuse amplitude with displacement in their answer and lost marks.
This was a demanding drawing requiring candidates to show the complex superposition of two waves. Some candidates rose well to this challenge, took their time, and drew very good attempts. Many however produced rather half-hearted and rushed diagrams that lost one or more marks for lack of quality. Teachers would be advised to study the mark scheme as it gives a sensible route for the construction of the final answer.

