| Date | May 2018 | Marks available | 2 | Reference code | 18M.2.HL.TZ2.1 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 2 |
| Command term | Show that | Question number | 1 | Adapted from | N/A |
Question
The ball is now displaced through a small distance x from the bottom of the bowl and is then released from rest.
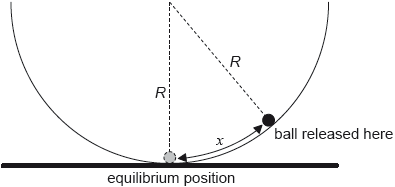
The magnitude of the force on the ball towards the equilibrium position is given by
\[\frac{{mgx}}{R}\]
where R is the radius of the bowl.
Outline why the ball will perform simple harmonic oscillations about the equilibrium position.
Show that the period of oscillation of the ball is about 6 s.
The amplitude of oscillation is 0.12 m. On the axes, draw a graph to show the variation with time t of the velocity v of the ball during one period.
Markscheme
the «restoring» force/acceleration is proportional to displacement
Direction is not required
[1 mark]
ω = «\(\sqrt {\frac{g}{R}} \)» = \(\sqrt {\frac{{9.81}}{{8.0}}} \) «= 1.107 s–1»
T = «\(\frac{{2\pi }}{\omega }\) = \(\frac{{2\pi }}{{1.107}}\) =» 5.7 «s»
Allow use of or g = 9.8 or 10
Award [0] for a substitution into T = 2π\(\sqrt {\frac{I}{g}} \)
[2 marks]
sine graph
correct amplitude «0.13 m s–1»
correct period and only 1 period shown
Accept ± sine for shape of the graph. Accept 5.7 s or 6.0 s for the correct period.
Amplitude should be correct to ±\(\frac{1}{2}\) square for MP2
eg: v /m s–1 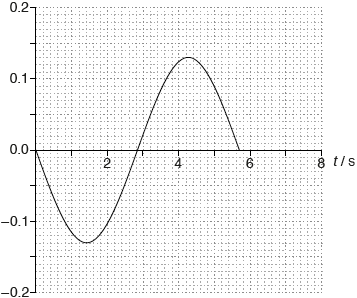
[3 marks]

