| Date | May 2018 | Marks available | 2 | Reference code | 18M.2.HL.TZ1.1 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 1 |
| Command term | Calculate | Question number | 1 | Adapted from | N/A |
Question
An elastic climbing rope is tested by fixing one end of the rope to the top of a crane. The other end of the rope is connected to a block which is initially at position A. The block is released from rest. The mass of the rope is negligible.
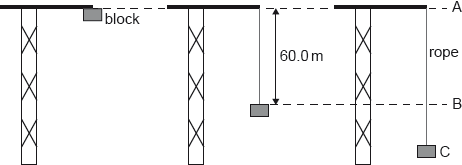
The unextended length of the rope is 60.0 m. From position A to position B, the block falls freely.
In another test, the block hangs in equilibrium at the end of the same elastic rope. The elastic constant of the rope is 400 Nm–1. The block is pulled 3.50 m vertically below the equilibrium position and is then released from rest.
Calculate the time taken for the block to return to the equilibrium position for the first time.
Calculate the speed of the block as it passes the equilibrium position.
Markscheme
T = 2π\(\sqrt {\frac{{80.0}}{{400}}} \) = 2.81 «s»
time = \(\frac{T}{4}\) = 0.702 «s»
Award [0] for kinematic solutions that assume a constant acceleration.
[2 marks]
ALTERNATIVE 1
ω = \(\frac{{2\pi }}{{2.81}}\) = 2.24 «rad s–1»
v = 2.24 × 3.50 = 7.84 «ms–1»
ALTERNATIVE 2
\(\frac{1}{2}\)kx2 = \(\frac{1}{2}\)mv2 OR \(\frac{1}{2}\)400 × 3.52 = \(\frac{1}{2}\)80v2
v = 7.84 «ms–1»
Award [0] for kinematic solutions that assume a constant acceleration.
Allow ECF for T from (e)(i).
[2 marks]

