| Date | May 2014 | Marks available | 2 | Reference code | 14M.2.HL.TZ2.7 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 2 |
| Command term | Determine | Question number | 7 | Adapted from | N/A |
Question
This question is about simple harmonic motion (SHM) and sound.
The diagram shows a section of continuous track of a long-playing (LP) record. The stylus (needle) is placed in the track of the record.
As the LP record rotates, the stylus moves because of changes in the width and position of the track. These movements are converted into sound waves by an electrical system and a loudspeaker.
A recording of a single-frequency musical note is played. The graph shows the variation in horizontal acceleration of the stylus with horizontal displacement.
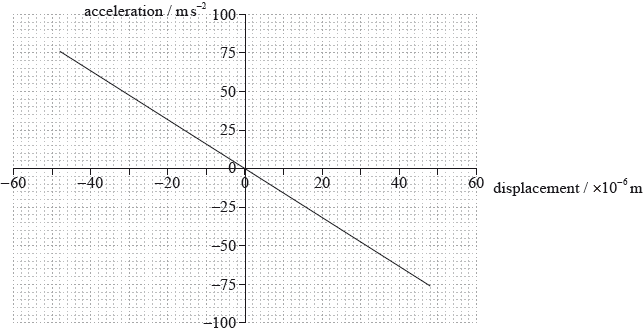
The mass of the stylus is \(5.5 \times {10^{ - 4}}{\text{ kg}}\). Determine the maximum kinetic energy of the stylus.
Markscheme
\({x_0} = 4.8 \times {10^{ - 5}}{\text{ (m)}}\);
\({E_{\text{k}}} = \frac{1}{2}m{\omega ^2}x_0^2 = 9.9 \times {10^{ - 7}}{\text{ (J)}}\)\(\,\,\,\)or\(\,\,\,\)\(1.0 \times {10^{ - 6}}{\text{ (J)}}\);
Allow [2] for a bald correct answer.

